 por claudia_r » Ter Out 06, 2009 11:05
por claudia_r » Ter Out 06, 2009 11:05
Estou com muita dificuldade para resolver esse exercício de P.A.
Numa P.A. de primeiro termo 1/3 e razão 1/2, a soma dos n primeios termos é 20/3. Determine o valor de n.
Encontrei o segundo termo da P.A. usando a fórmula do termo geral, já que tinha os dados de a1 e da razão. Depois peguei o resultado e joguei na fórmula da soma dos termos, mas não deu certo, ficou uma conta ridícula :/
-
claudia_r
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Ter Out 06, 2009 10:33
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por marciommuniz » Ter Out 06, 2009 13:08
por marciommuniz » Ter Out 06, 2009 13:08
A soma de uma P.A é dada por:
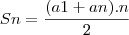
"Nunca penso no futuro, ele chega rápido demais." Albert Einsten
-
marciommuniz
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Qua Abr 08, 2009 20:06
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Metalúrgica UFF /Química Lic. UENF
- Andamento: cursando
Voltar para Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


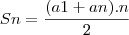



 , avisa que eu resolvo.
, avisa que eu resolvo.

