 por sphinx » Ter Mar 05, 2013 16:46
por sphinx » Ter Mar 05, 2013 16:46
Boa tarde pessoal, resolvi vários exercícios mas estou com duvida em algumas questões de geometria analítica, se puderem me ajudar a resolve-las, desde já agradeço.
1) Em um plano, munido de um sistema cartesiano ortogonal de referência, são dados os pontos A(2.3), B(9,4) e M(5,k). Determine o valor de k para o qual o ângulo BAM=45º
2) Dados os pontos A(3,0), B(1,0) e C(4+?3, 1+?3) calcular os ângulos internos do triângulo ABC
3) Conduzir por P(0,0) as retas que formam ângulo ?= ?/4 com r: 6x+2y-3=0
4) Determinar a reta s, simétrica de r: x-y+1=0 em relação a t: 2x+y+4=0
5) Os valores de m e k para os quais a equação mx²+y²+4x-6y+k=0 represente uma circunferência
-
sphinx
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Mar 05, 2013 16:44
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Eletrotecnica
- Andamento: cursando
 por Russman » Ter Mar 05, 2013 19:56
por Russman » Ter Mar 05, 2013 19:56
Você sabe tratar vetores? Tomando vetores nesse plano você resolve esses problemas.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por sphinx » Ter Mar 05, 2013 22:07
por sphinx » Ter Mar 05, 2013 22:07
Russman escreveu:Você sabe tratar vetores? Tomando vetores nesse plano você resolve esses problemas.
Como assim? poderia dar um exemplo?
Eu pensei na seguinte linha de raciocínio para resolver a primeira, mas não sei se está correto:
Utilizar a formula
Ya - Yb
Xa - Xb
para descobrir os coeficientes angulares e depois utilizar a formula
|mr-ms |
|1 + mr.ms |
pra descobrir o valor de K sabendo que a tg45º é 1
-
sphinx
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Mar 05, 2013 16:44
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Eletrotecnica
- Andamento: cursando
 por sauloandrade » Ter Mar 05, 2013 22:12
por sauloandrade » Ter Mar 05, 2013 22:12
O pensamento para a primeira questão está correto, você só precisa por a mão na massa

-
sauloandrade
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Dom Out 28, 2012 12:03
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Russman » Ter Mar 05, 2013 22:28
por Russman » Ter Mar 05, 2013 22:28
Na primeira questão se você construir os vetores

e
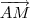
e fizer o produto interno de ambos fica fácil isolar o valor de

esperado. O produto interno dos mesmo é dado por
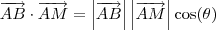
onde

é o angulo entre os vetores.
Pelas coordenadas, temos
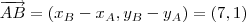
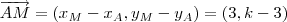
de modo que
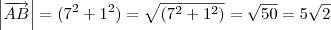
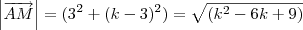
e portanto,
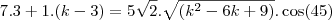
Agora é só resolver a equação em

.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Geomatria analitica] Duvidas questões!
por OoluanOo » Qui Mar 07, 2013 10:37
- 1 Respostas
- 1095 Exibições
- Última mensagem por Russman

Qui Mar 07, 2013 21:25
Geometria Analítica
-
- algumas duvidas
por Doc Brown » Sáb Jan 17, 2015 19:15
- 0 Respostas
- 1156 Exibições
- Última mensagem por Doc Brown

Sáb Jan 17, 2015 19:15
Equações
-
- [Probabilidade] Ajuda com algumas questões
por Duvidas » Dom Mai 17, 2015 12:53
- 0 Respostas
- 2778 Exibições
- Última mensagem por Duvidas

Dom Mai 17, 2015 12:53
Probabilidade
-
- algumas dúvidas urgentes!
por kika » Ter Nov 25, 2008 00:37
- 1 Respostas
- 2559 Exibições
- Última mensagem por kika

Qui Nov 27, 2008 06:54
Números Complexos
-
- Dúvidas de Geometria analítica
 por Priscila_moraes » Ter Nov 15, 2011 19:35
por Priscila_moraes » Ter Nov 15, 2011 19:35
- 1 Respostas
- 1321 Exibições
- Última mensagem por LuizAquino

Qua Nov 16, 2011 17:05
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




 e
e 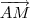 e fizer o produto interno de ambos fica fácil isolar o valor de
e fizer o produto interno de ambos fica fácil isolar o valor de  esperado. O produto interno dos mesmo é dado por
esperado. O produto interno dos mesmo é dado por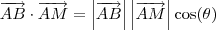
 é o angulo entre os vetores.
é o angulo entre os vetores.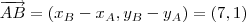
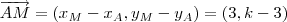
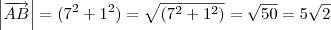
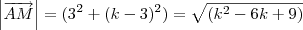
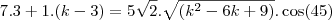
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.