PESSOAL TENHO DOIS EXERCICIOS DE TAXA DE VARIAÇÃO QUE NÃO CONSIGO FAZER, POR FAVOR ME AJUDEM COM ESSES EXERCICIOS POIS TEREI PROVA RELACIONADO A ESSE ASSUNTO E QUERIA VER A RESOLUÇÃO DESSAS 2 QUESTÕES! DESDE JÁ OBRIGADO.
1 - Um balão está a 60 m acima do solo e se eleva verticalmente à razão de 5 m/s. Um automóvel
passa por baixo do balão viajando à 12 m/s. Com que velocidade varia, um segundo depois, a
distância entre o balão e o automóvel?
2 - Despeja-se água num recipiente de forma cônica, à razão de 8 cm3/min. O cone tem 20 cm de
profundidade e 10 cm de diâmetro em sua parte superior. Se existe um furo na base, e o nível da
água está subindo à razão de 1 mm/min, com que velocidade a água estará escoando quando esta
estiver a 16 cm do fundo?


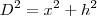
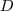 : distancia entre eles.
: distancia entre eles. : distancia do carro a vertical do balão.
: distancia do carro a vertical do balão. : altura do balão.
: altura do balão. 
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)