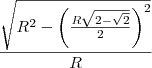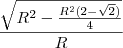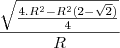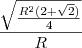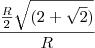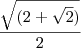por Georges123 » Sex Fev 15, 2013 10:52
por Georges123 » Sex Fev 15, 2013 10:52
![ln=\sqrt[]{2R²-r\sqrt[]{4R²-LN²}} ln=\sqrt[]{2R²-r\sqrt[]{4R²-LN²}}](/latexrender/pictures/eaaaed059e85ac13ac01bba6161caa5b.png)
( não considere esse  eu coloquei no editor e saiu assim é : ln=v2r²-rv4r²-ln²
COM essa fórmula eu tentei calcular o seno de 22,5 (22,5 mesmo e não 22,5º)
e encontrei
![\frac{\sqrt[]{2-\sqrt[]{2}}}{2} \frac{\sqrt[]{2-\sqrt[]{2}}}{2}](/latexrender/pictures/3f3ec9ad373da76348e7f8f1c4531da8.png)
( está correto?)
porem não consegui calcular o cosseno.
Ajude-me por favor
-
Georges123
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Sex Fev 15, 2013 10:41
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por young_jedi » Sex Fev 15, 2013 21:25
por young_jedi » Sex Fev 15, 2013 21:25
não sei se entendi bem mais se voce esta querendo calculo o seno e cosseno do angulo 22,5º
voce pode utilizar as seguintes relações
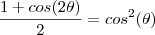
e
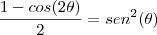
substituindo por 22,5º teremos
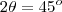
como esse angulo tem relações conhecidas de seno e cosseno voce consegue calcular
a equação que voce colocou

eu não sei oque ela significa não sei oque é r e ln se tivesse como voce demonstrar algo a respeito...
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Georges123 » Sex Fev 15, 2013 23:38
por Georges123 » Sex Fev 15, 2013 23:38

Esta é a fórmula de duplicação de arcos. Eu estou aprendendo a calcular por essa forma ( além de ser bem limitada usando os ângulos diretamente proporcionais a 30 45 e 60). Lembrando que o que sai do centro e encontra o lado perpendicularmente é o apótema.
CDEF É UM QUADRADO INSCRITO A CIRCUNFERÊNCIA E PORTANTO LN = 4
ln: número de lados
R: Raio.
-
Georges123
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Sex Fev 15, 2013 10:41
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Georges123 » Dom Fev 17, 2013 16:43
por Georges123 » Dom Fev 17, 2013 16:43
Desculpe mais a relação que você tirou com o cosseno de 22,5 eu não entendi, poderia me explicar de forma mais didática como você encontro o cosseno, pois é nele que eu me embolo

.
Por favor e muito obrigado
-
Georges123
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Sex Fev 15, 2013 10:41
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por young_jedi » Dom Fev 17, 2013 23:25
por young_jedi » Dom Fev 17, 2013 23:25
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Georges123 » Seg Mar 18, 2013 05:04
por Georges123 » Seg Mar 18, 2013 05:04
Olá eu fiquei com uma dúvida na resolução dessa conta:
![\frac{\sqrt[]{{\frac{R\sqrt[]{2-\sqrt[]{2}}}{2}}^{2}} - {R}^{2} }{R} \frac{\sqrt[]{{\frac{R\sqrt[]{2-\sqrt[]{2}}}{2}}^{2}} - {R}^{2} }{R}](/latexrender/pictures/24a9482c4cc80b760b77271f8fcdd635.png)
OBS: AQUELE 2 EM CIMA É AO QUADRADO.
que é o cosseno de 22,5º
-
Georges123
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Sex Fev 15, 2013 10:41
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por young_jedi » Seg Mar 18, 2013 17:56
por young_jedi » Seg Mar 18, 2013 17:56
acho que a equação é esta, certo?
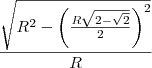
primeiro elevando oque esta no parentese ao quadrado
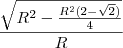
tirando o minimo multiplo do que esta na raiz temos
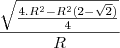
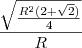
tirando o R^2 e o 4 da raiz
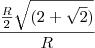
simplificando os R
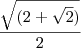
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Georges123 » Dom Mar 24, 2013 00:17
por Georges123 » Dom Mar 24, 2013 00:17
Entendi muito obrigado.
-
Georges123
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Sex Fev 15, 2013 10:41
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Geometria Plana
por claudia » Qui Out 23, 2008 16:11
- 1 Respostas
- 8726 Exibições
- Última mensagem por admin

Ter Out 28, 2008 16:47
Geometria Plana
-
- Geometria plana
por Rayanne07 » Qua Jan 13, 2010 17:40
- 3 Respostas
- 4721 Exibições
- Última mensagem por Rayanne07

Sex Jan 15, 2010 10:46
Geometria Plana
-
- Geometria Plana
 por MelvinMyster » Sex Ago 13, 2010 10:07
por MelvinMyster » Sex Ago 13, 2010 10:07
- 1 Respostas
- 4829 Exibições
- Última mensagem por alexandre32100

Sex Ago 13, 2010 13:15
Geometria Plana
-
- Geometria plana
 por Paulo A G » Qua Jan 26, 2011 16:11
por Paulo A G » Qua Jan 26, 2011 16:11
- 0 Respostas
- 2542 Exibições
- Última mensagem por Paulo A G

Qua Jan 26, 2011 16:11
Geometria Plana
-
- geometria plana
 por Abner » Seg Jan 31, 2011 17:53
por Abner » Seg Jan 31, 2011 17:53
- 3 Respostas
- 3683 Exibições
- Última mensagem por Abner

Ter Fev 01, 2011 17:31
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![ln=\sqrt[]{2R²-r\sqrt[]{4R²-LN²}} ln=\sqrt[]{2R²-r\sqrt[]{4R²-LN²}}](/latexrender/pictures/eaaaed059e85ac13ac01bba6161caa5b.png) ( não considere esse  eu coloquei no editor e saiu assim é : ln=v2r²-rv4r²-ln²
( não considere esse  eu coloquei no editor e saiu assim é : ln=v2r²-rv4r²-ln²![\frac{\sqrt[]{2-\sqrt[]{2}}}{2} \frac{\sqrt[]{2-\sqrt[]{2}}}{2}](/latexrender/pictures/3f3ec9ad373da76348e7f8f1c4531da8.png) ( está correto?)
( está correto?)
![ln=\sqrt[]{2R²-r\sqrt[]{4R²-LN²}} ln=\sqrt[]{2R²-r\sqrt[]{4R²-LN²}}](/latexrender/pictures/eaaaed059e85ac13ac01bba6161caa5b.png) ( não considere esse  eu coloquei no editor e saiu assim é : ln=v2r²-rv4r²-ln²
( não considere esse  eu coloquei no editor e saiu assim é : ln=v2r²-rv4r²-ln²![\frac{\sqrt[]{2-\sqrt[]{2}}}{2} \frac{\sqrt[]{2-\sqrt[]{2}}}{2}](/latexrender/pictures/3f3ec9ad373da76348e7f8f1c4531da8.png) ( está correto?)
( está correto?)
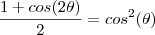
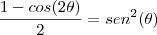
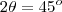




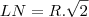
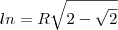
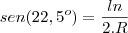
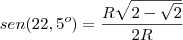
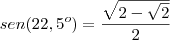
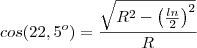
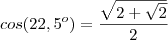


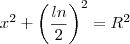
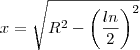
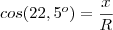
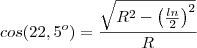

![\frac{\sqrt[]{{\frac{R\sqrt[]{2-\sqrt[]{2}}}{2}}^{2}} - {R}^{2} }{R} \frac{\sqrt[]{{\frac{R\sqrt[]{2-\sqrt[]{2}}}{2}}^{2}} - {R}^{2} }{R}](/latexrender/pictures/24a9482c4cc80b760b77271f8fcdd635.png)