 por ViniRFB » Qui Jan 31, 2013 02:01
por ViniRFB » Qui Jan 31, 2013 02:01
Quantos números inteiros n satisfazem a sentença
Alguém pode resolver essa questão passo a passo, pois achei o resultado, mas creio que fiz algo errado.
Grato.
Reposta 10
1 <
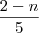
menor igual a 3
N sei o usar o latex code para símbolo menor igual ou maior igual
-
ViniRFB
- Usuário Parceiro

-
- Mensagens: 76
- Registrado em: Dom Fev 19, 2012 22:16
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por young_jedi » Qui Jan 31, 2013 15:27
por young_jedi » Qui Jan 31, 2013 15:27
o equação é esta
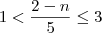
primeiro voce resolve a primeira equação
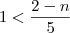
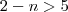
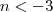
e agora a segunda equaçaõ
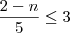
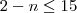
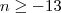
como n deve ser inteiro então n pode ser qualquer numero inteiro entre
-3 e -13
mais ele tambem por ser -13, porem não pode ser -3
logo nos temos
-4 -5 -6 -7 -8 -9 -10 -11 -12 -13
10 numeros
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por DanielFerreira » Qui Jan 31, 2013 22:58
por DanielFerreira » Qui Jan 31, 2013 22:58
Outra forma de resolver:
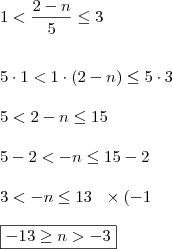
ou,
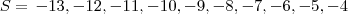 ViniRFB
ViniRFB,
quanto ao LaTeX, Pode recorrer ao
Editor de Fórmulas que fica na barra acima.
Espero também ter ajudado!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por ViniRFB » Sex Fev 01, 2013 10:32
por ViniRFB » Sex Fev 01, 2013 10:32
Obrigado aos dois colaboradores.
Ainda resta uma dúvida na resposta de Young as desigualdades não betem com Danjr, por quê?
-
ViniRFB
- Usuário Parceiro

-
- Mensagens: 76
- Registrado em: Dom Fev 19, 2012 22:16
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por young_jedi » Sex Fev 01, 2013 12:04
por young_jedi » Sex Fev 01, 2013 12:04
na ultima passagem do
danjr5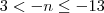
multiplicando por -1
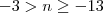
o
danjr5 de inverteu o -3 e o -13 deve ter sido erro de digitação
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por ViniRFB » Sex Fev 01, 2013 19:46
por ViniRFB » Sex Fev 01, 2013 19:46
Pois é...
Fiz novamente e notei isso.
Grato amigos e bom final de semana a todos.
-
ViniRFB
- Usuário Parceiro

-
- Mensagens: 76
- Registrado em: Dom Fev 19, 2012 22:16
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por DanielFerreira » Sex Fev 01, 2013 21:03
por DanielFerreira » Sex Fev 01, 2013 21:03
young_jedi escreveu:o danjr5 de inverteu o -3 e o -13 deve ter sido erro de digitação
Não foi não
Young_jedi, errei mesmo [risos]! Agradeço a correção.
ViniRFB,
desculpe-me pelo equívoco.
Até logo.
Daniel F.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Inequações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Inequações
por Bruno 888 » Qua Set 24, 2008 20:36
- 1 Respostas
- 4216 Exibições
- Última mensagem por admin

Ter Set 30, 2008 17:09
Inequações
-
- Inequações
por Rose » Seg Nov 24, 2008 22:44
- 2 Respostas
- 3696 Exibições
- Última mensagem por Rose

Qua Nov 26, 2008 08:18
Inequações
-
- Inequações
 por cristina » Seg Set 07, 2009 01:46
por cristina » Seg Set 07, 2009 01:46
- 2 Respostas
- 2926 Exibições
- Última mensagem por cristina

Seg Set 07, 2009 20:55
Sistemas de Equações
-
- inequações
por jose henrique » Ter Out 26, 2010 23:56
- 10 Respostas
- 6830 Exibições
- Última mensagem por MarceloFantini

Qui Nov 04, 2010 10:31
Sistemas de Equações
-
- Inequações
por brijahh » Sáb Ago 06, 2011 10:38
- 1 Respostas
- 2213 Exibições
- Última mensagem por MarceloFantini

Sáb Ago 06, 2011 17:00
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
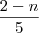 menor igual a 3
menor igual a 3
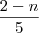 menor igual a 3
menor igual a 3
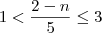
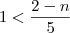
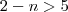
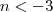
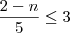
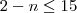
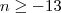

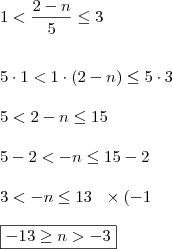
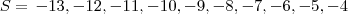


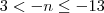
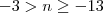



 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
