Estou desconfiado que existe um erro de digitação na resposta do livro do Stewart 5ª edição.
Na página 191 quesito 23 tem a seguinte questão:
Diferencie a função:
![y= \frac{{x}^{2}+4x+3}{\sqrt[]{x}} y= \frac{{x}^{2}+4x+3}{\sqrt[]{x}}](/latexrender/pictures/b17bfdb363647ab6af1c1a81994d4138.png)
Resposta do livro:
![y'= \frac{3}{2}\sqrt[]{x}+\frac{2}{\sqrt[]{x}}-\frac{\frac{3}{2x}}{\sqrt[]{x}} y'= \frac{3}{2}\sqrt[]{x}+\frac{2}{\sqrt[]{x}}-\frac{\frac{3}{2x}}{\sqrt[]{x}}](/latexrender/pictures/b57755a15847f99866a7a91f0ce9066a.png)
Minha resposta:
![y'= \frac{3}{2}\sqrt[]{x}+\frac{2}{\sqrt[]{x}}-\frac{\frac{3}{2}}{\sqrt[]{x}} y'= \frac{3}{2}\sqrt[]{x}+\frac{2}{\sqrt[]{x}}-\frac{\frac{3}{2}}{\sqrt[]{x}}](/latexrender/pictures/7621a18c04278ca7c6a978c5a955625a.png)
Observe que a resposta está muito parecida porém ao invés de dar:
![-\frac{\frac{3}{2x}}{\sqrt[]{x}} -\frac{\frac{3}{2x}}{\sqrt[]{x}}](/latexrender/pictures/24b8aebf4b0160c93f3dfbd83595bcdb.png) como diz o livro, minha resposta deu:
como diz o livro, minha resposta deu: ![-\frac{\frac{3}{2}}{\sqrt[]{x}} -\frac{\frac{3}{2}}{\sqrt[]{x}}](/latexrender/pictures/440566b149c546b285b82d1c700666f6.png)
Observe ainda que o Stewart está dizendo que:
![-\frac{\frac{3}{2\sqrt[]{x}}}{x} -\frac{\frac{3}{2\sqrt[]{x}}}{x}](/latexrender/pictures/725590f7876e4c3ecfe5dd4b974680c8.png) =
= ![-\frac{\frac{3}{2x}}{\sqrt[]{x}} -\frac{\frac{3}{2x}}{\sqrt[]{x}}](/latexrender/pictures/24b8aebf4b0160c93f3dfbd83595bcdb.png) .
. Mas na verdade
![-\frac{\frac{3}{2\sqrt[]{x}}}{x} -\frac{\frac{3}{2\sqrt[]{x}}}{x}](/latexrender/pictures/725590f7876e4c3ecfe5dd4b974680c8.png) =
= ![-\frac{\frac{3}{2}}{\sqrt[]{x}} -\frac{\frac{3}{2}}{\sqrt[]{x}}](/latexrender/pictures/440566b149c546b285b82d1c700666f6.png) .
.Eu não escrevi tudo que eu desenvolvi aqui porque iria demorar muito, mas ao invés de usar a regra do quociente direto, eu primeiro reescrevi a função para:
![y= \frac{{x}^{2}}{{x}^{\frac{1}{2}}}+4\frac{x}{{x}^{\frac{1}{2}}}+\frac{3}{\sqrt[]{x}} y= \frac{{x}^{2}}{{x}^{\frac{1}{2}}}+4\frac{x}{{x}^{\frac{1}{2}}}+\frac{3}{\sqrt[]{x}}](/latexrender/pictures/bec2c7feec48d22675f80563da78fb00.png)
daí então eu derivei utilizando a regra da potência em
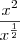 e em
e em 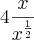 utilizando a propriedade da potência antes claro, e em seguida utilizei a regra do quociente em
utilizando a propriedade da potência antes claro, e em seguida utilizei a regra do quociente em ![\frac{3}{\sqrt[]{x}} \frac{3}{\sqrt[]{x}}](/latexrender/pictures/5fa4bad81ab75160f55c799db164c6c3.png) .
.Daí foi só desenvolver e chegar na resposta mencionada acima.


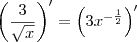
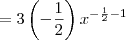

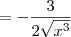
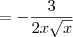


![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.