 por e8group » Sex Dez 21, 2012 11:26
por e8group » Sex Dez 21, 2012 11:26
Suponha que
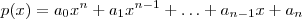
seja um polinômio de grau

com coeficientes inteiros , isto é ,
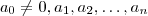
são números inteiros .Seja

um número inteiro .Prove que se

for raiz de
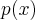
,então

será divisor do termo independente
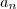
.
Solução :
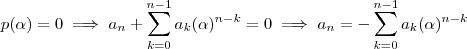
Como
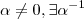
. Então ,
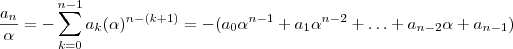
.
Se
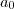
é inteiro ,
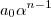
resulta um número inteiro , pois

é inteiro
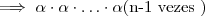
é inteiro . Assim,
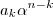
é inteiro para
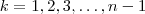
.Logo ,
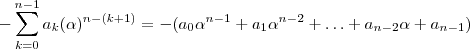
é um número inteiro e portanto
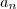
é divisível por

.
A solução estar certa ? Ou não ? Se não ,como poderia provar isto ?
Agradeço desde já !
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por e8group » Sex Dez 21, 2012 12:07
por e8group » Sex Dez 21, 2012 12:07
Pessoal cometi um erro sutil em assumir
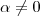
.Pois

é inteiro . Vamos supor então que a solução acima vale somente para

inteiro não nulo . Este será o primeiro caso . E no segundo caso ,vamos assumir que

.
Assim temos ,
caso 1 : (
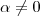
)
Corresponde a minha primeira solução ...
caso 2(

)
Temos que provar ,peço ajuda de vc's .
Agora estar coerente (eu acho ).
Se a resposta acima estiver correta , como ficaria o caso 2 ?
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por young_jedi » Sex Dez 21, 2012 15:08
por young_jedi » Sex Dez 21, 2012 15:08
acho que seu pensamento esta certo sim
no entanto para

, acho que não se aplica
mesmo porque em um polinomio de grau qualquer, se 0 é raiz deste polinomio, então ele não possui termo independente, ou seja todos os termos tem uma potencia de x
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por e8group » Sáb Dez 22, 2012 10:46
por e8group » Sáb Dez 22, 2012 10:46
young_jedi ,muito obrigado pela ajuda .Como o enunciado diz que

é inteiro e

é inteiro .Vou utilizar o seu argumento ,se

o termo independente é nulo .Logo ,neste caso não se aplica .Além disso , estaríamos efetuando a divisão "0/0" .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Polinômios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Prove: n(A X B) = n(A) * n(B)
por juliomarcos » Dom Set 14, 2008 02:58
- 3 Respostas
- 5286 Exibições
- Última mensagem por admin

Qua Set 24, 2008 05:33
Conjuntos
-
- Prove que
por Balanar » Dom Ago 29, 2010 17:22
- 1 Respostas
- 2317 Exibições
- Última mensagem por MarceloFantini

Seg Ago 30, 2010 01:24
Álgebra Elementar
-
- Prove
por chronoss » Dom Abr 21, 2013 16:52
- 3 Respostas
- 3075 Exibições
- Última mensagem por chronoss

Seg Abr 22, 2013 14:23
Álgebra Elementar
-
- Prove
por chronoss » Seg Abr 29, 2013 20:40
- 1 Respostas
- 1989 Exibições
- Última mensagem por chronoss

Sáb Mai 04, 2013 13:55
Álgebra Elementar
-
- PROVE
por pedro22132938 » Sex Ago 21, 2015 20:10
- 1 Respostas
- 2833 Exibições
- Última mensagem por e8group

Dom Ago 23, 2015 20:21
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
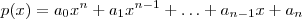 seja um polinômio de grau
seja um polinômio de grau  com coeficientes inteiros , isto é ,
com coeficientes inteiros , isto é , 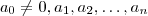 são números inteiros .Seja
são números inteiros .Seja  um número inteiro .Prove que se
um número inteiro .Prove que se  for raiz de
for raiz de 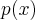 ,então
,então  será divisor do termo independente
será divisor do termo independente 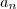 .
. 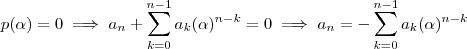
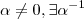 . Então ,
. Então , 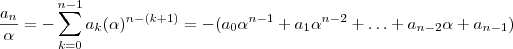 .
. 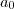 é inteiro ,
é inteiro , 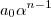 resulta um número inteiro , pois
resulta um número inteiro , pois  é inteiro
é inteiro 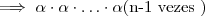 é inteiro . Assim,
é inteiro . Assim, 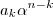 é inteiro para
é inteiro para 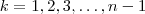 .Logo ,
.Logo , 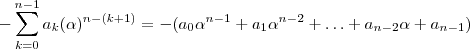 é um número inteiro e portanto
é um número inteiro e portanto 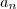 é divisível por
é divisível por  .
.

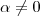 .Pois
.Pois  .
.  , acho que não se aplica
, acho que não se aplica é inteiro .Vou utilizar o seu argumento ,se
é inteiro .Vou utilizar o seu argumento ,se 

 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.