 por Gustavo Gomes » Qua Dez 12, 2012 22:04
por Gustavo Gomes » Qua Dez 12, 2012 22:04
Olá, pessoal.
Seja

. Qual o menor valor de
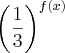
?
A resposta é 9.
Desenvolvendo a expressão, cheguei em
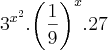
, mas daí não consegui pensar em um valor mínimo para essa expressão, para
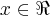
....
Aguardo. Grato.
-
Gustavo Gomes
- Usuário Parceiro

-
- Mensagens: 50
- Registrado em: Sex Out 05, 2012 22:05
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matemática-Licenciatura
- Andamento: formado
 por Russman » Qua Dez 12, 2012 22:58
por Russman » Qua Dez 12, 2012 22:58
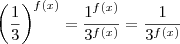
Note que essa expressão,
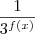
, irá atingir seu menor valor quanto maior for o seu denominador. Assim, temos de maximizar o termo
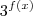
. Para isto temos de encontrar o maior valor que

pode atingir!
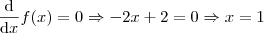
Sabemos que a função atinge seu máximo/mínimo em

e este valor corresponde a
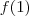
.
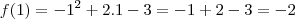
Portanto,
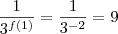
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Função exponencial] Exercício sobre função exponencial
por fff » Ter Jan 07, 2014 17:51
- 3 Respostas
- 4079 Exibições
- Última mensagem por fff

Qua Jan 08, 2014 06:47
Funções
-
- [Desigualdade] entre função exponencial e função potência
por VitorFN » Sex Mai 26, 2017 15:18
- 1 Respostas
- 5751 Exibições
- Última mensagem por adauto martins

Sex Jul 07, 2017 12:17
Álgebra Elementar
-
- [função exponencial] Exprimir em função de x
por fff » Ter Jan 07, 2014 12:02
- 2 Respostas
- 3132 Exibições
- Última mensagem por fff

Ter Jan 07, 2014 13:23
Funções
-
- funçao exponencial ITA
por zeramalho2004 » Dom Jun 28, 2009 19:55
- 3 Respostas
- 5129 Exibições
- Última mensagem por Marcampucio

Seg Jun 29, 2009 15:23
Funções
-
- Função Exponencial
por Aline » Seg Jun 29, 2009 18:59
- 3 Respostas
- 5910 Exibições
- Última mensagem por Cleyson007

Qua Jul 01, 2009 22:59
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 . Qual o menor valor de
. Qual o menor valor de 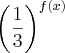 ?
?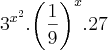 , mas daí não consegui pensar em um valor mínimo para essa expressão, para
, mas daí não consegui pensar em um valor mínimo para essa expressão, para 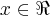 ....
....
 . Qual o menor valor de
. Qual o menor valor de 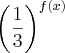 ?
?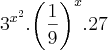 , mas daí não consegui pensar em um valor mínimo para essa expressão, para
, mas daí não consegui pensar em um valor mínimo para essa expressão, para 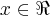 ....
....
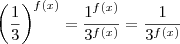
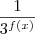 , irá atingir seu menor valor quanto maior for o seu denominador. Assim, temos de maximizar o termo
, irá atingir seu menor valor quanto maior for o seu denominador. Assim, temos de maximizar o termo 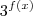 . Para isto temos de encontrar o maior valor que
. Para isto temos de encontrar o maior valor que  pode atingir!
pode atingir!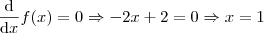
 e este valor corresponde a
e este valor corresponde a 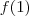 .
.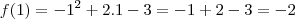
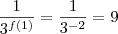



 , avisa que eu resolvo.
, avisa que eu resolvo.

