Seja
. Qual o menor valor de 
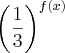?A resposta é 9.
Desenvolvendo a expressão, cheguei em
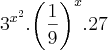, mas daí não consegui pensar em um valor mínimo para essa expressão, para 
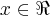....Aguardo. Grato.
por Gustavo Gomes » Qua Dez 12, 2012 22:04
. Qual o menor valor de 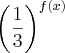?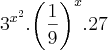, mas daí não consegui pensar em um valor mínimo para essa expressão, para ....
por Russman » Qua Dez 12, 2012 22:58
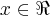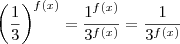
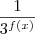, irá atingir seu menor valor quanto maior for o seu denominador. Assim, temos de maximizar o termo 
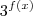. Para isto temos de encontrar o maior valor que 
pode atingir!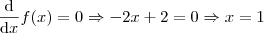
e este valor corresponde a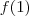 
.
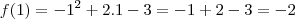
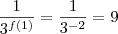
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
(dica : igualar a expressão a 
e elevar ao quadrado os dois lados)