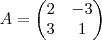
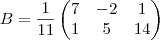
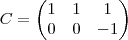
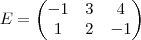
Sabendo que a matriz D=A*B, determinar a matriz X tal que:
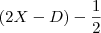 (E+C) = O
(E+C) = O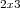
A, B, C e E são matrizes reais.
Primeiro não consigo calcular a A*B devido a ter a fração
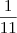 na matriz B
na matriz BSegundo não tenho mesmo a mínima ideia de como se calcula o X, depois também não sei o que significa o O no final
Alguém me pode ajudar? Ou então resolver para eu ver como se faz?


 faça como uma multiplicação normal de matrizes, e depois multiplique todos os elementos por
faça como uma multiplicação normal de matrizes, e depois multiplique todos os elementos por 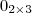 quer dizer a matriz nula com duas linhas e três colunas, ou
quer dizer a matriz nula com duas linhas e três colunas, ou 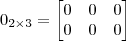 .
. resolva normalmente:
resolva normalmente: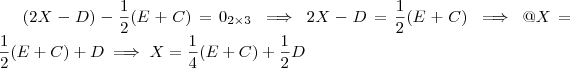 .
. é tranquilo, basta somar componente a componente. O que dá um pouco mais de trabalho é a matriz
é tranquilo, basta somar componente a componente. O que dá um pouco mais de trabalho é a matriz 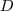 . Depois é só multiplicar pelos respectivos coeficientes e terá completado a solução.
. Depois é só multiplicar pelos respectivos coeficientes e terá completado a solução.

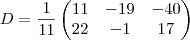
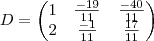
![\frac{1}{2} (X+A) = 3[X+(A-X)]+E \frac{1}{2} (X+A) = 3[X+(A-X)]+E](/latexrender/pictures/af125c81e8f4d6499ab763bb43afdfb4.png) aqui tenho 3 X, como arranjo forma de os calcular?
aqui tenho 3 X, como arranjo forma de os calcular?![\frac{1}{3}(AE^T+X) = 2CI+\frac{1}{6}[X+(A-X)-A] \frac{1}{3}(AE^T+X) = 2CI+\frac{1}{6}[X+(A-X)-A]](/latexrender/pictures/999a0b1be12f14096953face00d1d3a6.png)
![\frac{1}{2}(X+A) = 3[X + (A-X)] +E \frac{1}{2}(X+A) = 3[X + (A-X)] +E](/latexrender/pictures/a39ab71f9fa41cf84d344c4d9317849c.png) , note que
, note que  , logo ela torna-se
, logo ela torna-se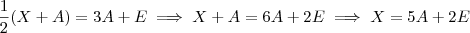 .
.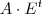 não é possível pois
não é possível pois 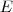 é uma matriz
é uma matriz 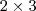 , logo
, logo 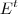 é uma matriz
é uma matriz 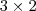 . Como o número de linhas é diferente do número de colunas a multiplicação não é possível.
. Como o número de linhas é diferente do número de colunas a multiplicação não é possível.
 .
.
 :
: