Opa, beleza galera?
estou com um exercício que está me complicando , mas acredito que ele não seja dos mais complicadoos para quem já tenha algum conhecimento de elipse.
Ele quer que eu obtenha a equação da elipse com os dados que ele dá:
a) eixo maior =10 , F1(2,-1) F2(2,5)
b)Vértices A1(0,6) ,A2(0,-6) e passando pelo ponto P(3,2)
c)F1(-1,3) , F2(-1,5) e excnetricidade = 2/3
----->Na letra a, o eixo maior sendo igual a 10, obtenho que a=5 , correto?
E dos dois focos tiro a relação de que 2c=6, logo o c=3
a²=b²+c²
25-9= b²
b=+/- 4
Centro( 2,2)
OBs: eu achei o Centro através do esboço prévio da elipse, não sei se tem algum processo algébrico para descobrir.
(x-2)²/16 + (y-2)²/25=1
25(x² + 4 -4x) + 16(y² + 4 -4y) = 1
25x² -100x +16y² -64y +(164-1) = 0
25x² -100x + 16y² - 64y + 163= 0
porém, o resultado dá: 25x² - 100x + 16y² - 64y - 236
De onde saiu esse 236 ?? fiquei totalmente perdido nessa parte.
-----> Na letra b
2a=12 , a=6
eu penso que como P pertence a elipse , eu faria:
9/a² + 4/36 = 1
só que achho que não é assim, pois chego que a² = raiz de 81/8
------> letra C tá dífícil de começar, pois só sei que 2c=4 , c=2
e da excentricidade eu não sei quanto é c, pois sei que ele é 2, mas na fórmula aparece c/a = 3/2










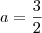
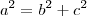




 +
+  = 720
= 720![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.