 por renan_a » Qua Nov 14, 2012 19:23
por renan_a » Qua Nov 14, 2012 19:23
Determinar a equação reduzida, o vértice, o foco, uma eq da diretriz e uma equação do eixo da parábola da equação dada:
X² - 2x -20y - 39 = 0
Bom, para achar a equação reduzida eu isolei os ''x' de uma lado e deixei os ''y'' do outro
x² - 2x= 20y + 39
(x-1)² = 20y + 39 + 1
(x-1)² = 20(y+2)
logo, sei que a euqação seria: x²= 20y
Como o vértice é (h,k) , V(1,-2)
-------------------
Através da comparação tenho que :
2p=20 -> p=10 -> p/2=5
Só que não sei como descobrir o FOCO, equação da diretriz e nem a equação do eixo.
eu teria que desenhar a parábola somente com a euqação e o vértice, e 'pela lógica fazer os valores do foco ?
sei que a ordenada do foco seria 5, correto? mas como eu descubro a abcissa?
-
renan_a
- Usuário Dedicado

-
- Mensagens: 32
- Registrado em: Ter Set 25, 2012 08:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecânica
- Andamento: cursando
 por young_jedi » Qua Nov 14, 2012 22:26
por young_jedi » Qua Nov 14, 2012 22:26
Em coordenadas cartesianas, uma parábola com um eixo paralelo ao eixo y com vértice (h, k), foco (h, k + p), e diretriz y = k - p, com p sendo a distância entre o vértice e o foco, possui a equação:

comparando com a equação que voce encontrou
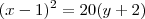
então

p=5
portanto seu foco sera
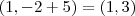
e sua diretriz sera
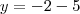
y=-7
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por renan_a » Sex Nov 16, 2012 09:51
por renan_a » Sex Nov 16, 2012 09:51
Obrigado, deu certinho. Tinha conseguido fazer pela lógica, mas em matemática somente a lógica nunca é o bastante.
Como é difícil achar um livro bom de geometria analítica, pois no que eu uso não diz nada sobre achar o fooco e diretriz desse modo que tu ensinou.]abraço
-
renan_a
- Usuário Dedicado

-
- Mensagens: 32
- Registrado em: Ter Set 25, 2012 08:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecânica
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Cônicas: Parábola]
por Ana_Rodrigues » Sáb Nov 19, 2011 11:39
- 1 Respostas
- 1621 Exibições
- Última mensagem por LuizAquino

Dom Nov 20, 2011 12:19
Geometria Analítica
-
- cônicas:equação da parabola
por may » Ter Jul 12, 2011 21:35
- 2 Respostas
- 11436 Exibições
- Última mensagem por may

Sex Jul 15, 2011 00:46
Geometria Analítica
-
- [Cônicas] 2 exerícios de parábola
por renan_a » Sex Nov 16, 2012 10:00
- 3 Respostas
- 3802 Exibições
- Última mensagem por young_jedi

Sex Nov 16, 2012 14:40
Geometria Analítica
-
- [Cônicas] O lugar geométrico dos vértices da parábola.
por Matheus Brito 2014 » Qui Set 10, 2015 22:40
- 1 Respostas
- 1587 Exibições
- Última mensagem por nakagumahissao

Sex Set 11, 2015 14:47
Geometria Analítica
-
- [Cônicas]Retas tangentes à cônicas
por Hopkins » Ter Fev 28, 2017 22:39
- 0 Respostas
- 1531 Exibições
- Última mensagem por Hopkins

Ter Fev 28, 2017 22:39
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




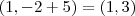



 , avisa que eu resolvo.
, avisa que eu resolvo.

