Determinar a equação reduzida, o vértice, o foco, uma eq da diretriz e uma equação do eixo da parábola da equação dada:
X² - 2x -20y - 39 = 0
Bom, para achar a equação reduzida eu isolei os ''x' de uma lado e deixei os ''y'' do outro
x² - 2x= 20y + 39
(x-1)² = 20y + 39 + 1
(x-1)² = 20(y+2)
logo, sei que a euqação seria: x²= 20y
Como o vértice é (h,k) , V(1,-2)
-------------------
Através da comparação tenho que :
2p=20 -> p=10 -> p/2=5
Só que não sei como descobrir o FOCO, equação da diretriz e nem a equação do eixo.
eu teria que desenhar a parábola somente com a euqação e o vértice, e 'pela lógica fazer os valores do foco ?
sei que a ordenada do foco seria 5, correto? mas como eu descubro a abcissa?



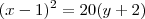

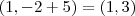
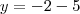

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)