







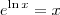 e
e 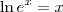 .
.


 tem como oposto
tem como oposto 
 tem como inverso
tem como inverso 
 tem como inverso
tem como inverso 
 será a base e a variável
será a base e a variável  passa ser o expoente, então...
passa ser o expoente, então... tem como inverso
tem como inverso 
 e sei também quanto vale
e sei também quanto vale  , mas a minha incógnita é o
, mas a minha incógnita é o  !"
!" ".
". seja algum tipo de grandeza... caso vc deseje ampliá-la, o que vc faz? Uma solução é multiplicar
seja algum tipo de grandeza... caso vc deseje ampliá-la, o que vc faz? Uma solução é multiplicar  por um coeficiente
por um coeficiente  , se
, se  , então vc terá três vezes o valor orignal da grandeza (
, então vc terá três vezes o valor orignal da grandeza ( ), outra solução é fazer
), outra solução é fazer 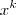 , isso é o que chamamos de crescimento ou decrescimento exponencial, pois se
, isso é o que chamamos de crescimento ou decrescimento exponencial, pois se  , então o valor dessa grandeza não será somado com outro valor igual ao dela, será multiplicado por outro valor igual ao dela
, então o valor dessa grandeza não será somado com outro valor igual ao dela, será multiplicado por outro valor igual ao dela  !
! é igual a
é igual a  . Já quando ver um
. Já quando ver um  , pense assim: quantas vezes o valor 10 precisa ser multiplicado por ele mesmo para dar o resultado 1000!?
, pense assim: quantas vezes o valor 10 precisa ser multiplicado por ele mesmo para dar o resultado 1000!? ! A maioria diz que ela é importante mas não sabem explicar o porque... a melhor explicação que dão é que a taxa de variação de
! A maioria diz que ela é importante mas não sabem explicar o porque... a melhor explicação que dão é que a taxa de variação de 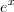 é
é 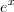 , como se isso dissesse tudo!
, como se isso dissesse tudo!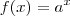 , mas quando vc define
, mas quando vc define  passa ter a vantagem de poder enchegar a tx de variação da sua função, que será
passa ter a vantagem de poder enchegar a tx de variação da sua função, que será  a tx de variação é
a tx de variação é  .
. também estabelece algumas relações bem interessantes entre a derivada tradicional e a derivada geométrica, recomendo vc pesquisar por Multiplicative Calculus.
também estabelece algumas relações bem interessantes entre a derivada tradicional e a derivada geométrica, recomendo vc pesquisar por Multiplicative Calculus.
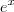 é igual ao proprio
é igual ao proprio 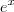 ? Se considerarmos o termo " a " da função exponencial sendo igual a
? Se considerarmos o termo " a " da função exponencial sendo igual a  então porque que o termo "a" sobe para o expoente e multiplica o "x" igual vc colocou?
então porque que o termo "a" sobe para o expoente e multiplica o "x" igual vc colocou?  porem, nós haviamos considerado que o "a " seria igual a "e" , pq que o "a" subiu para o expoente?
porem, nós haviamos considerado que o "a " seria igual a "e" , pq que o "a" subiu para o expoente?
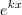 .
.

 para o expoente, eu defini
para o expoente, eu defini  como sendo o expoente.
como sendo o expoente.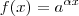 , como
, como  , com
, com  , então vc está diante duma P.G. de razão igual a
, então vc está diante duma P.G. de razão igual a  . Bem... acho que isso é o meu supra sumo sobre o assunto!
. Bem... acho que isso é o meu supra sumo sobre o assunto!
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
zig escreveu:

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.