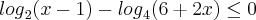
Mudando o segundo termo de base eu fiz:
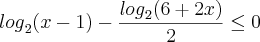
Que fica:
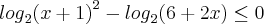
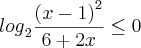
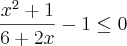
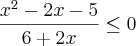

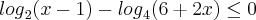
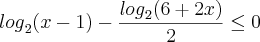
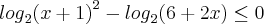
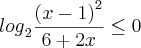
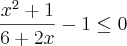
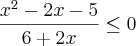

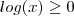 se
se 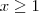 e
e 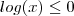 se
se 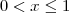
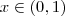 ,
, 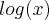 é sempre menor que zero . Basta pegar valores testes , como por exemplo ,
é sempre menor que zero . Basta pegar valores testes , como por exemplo , 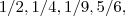 e por aí vai .
e por aí vai . 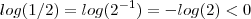 .De fato
.De fato 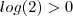 mas como temos
mas como temos  multiplicando o mesmo , logo concluímos que
multiplicando o mesmo , logo concluímos que  .
. 
santhiago escreveu:Estar quase certo , você cometeu um erro assumindo que o logaritmando é menor ou igual a zero , isto não é verdade .O que é verdade que o logaritmo neste contexto é menor ou igual a zero . Diante disso você deve analisar o intervalo para o logaritmando para a qual uma função função logarítmica é menor ou igual a zero .
Em Geral ,se
e
se
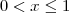
Tente aplicar este conceito a este exercício .
Talvez analisar o comportamento da função exponencial é mais fácil , e lembrando que a função logartimica é a inversa da exponencial .
Perceba que,
é sempre menor que zero . Basta pegar valores testes , como por exemplo ,
e por aí vai .
Veja ,.De fato
mas como temos
multiplicando o mesmo , logo concluímos que
.
No mais você acertou , você omitiu o 2 no denominador . Mas tudo bem , como o denominador é fixo e maior que zero . O quociente será menor ou igual a zero se e somente se o numerador é menor ou igual a zero .
Se tiver dúvidas post algo .

 tal que
tal que 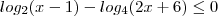 .
. 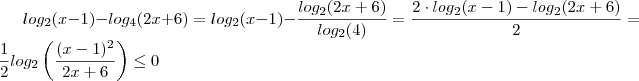
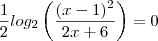
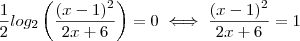
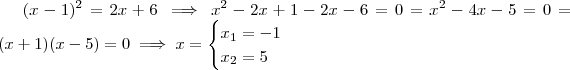 .
. 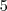 .
. 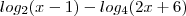 . Caso assumirmos
. Caso assumirmos 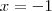 estamos entrando em contradição com a definição .
estamos entrando em contradição com a definição . 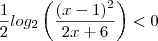
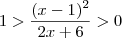
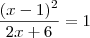 quando
quando  , ou seja
, ou seja 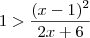 quando
quando 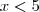 .
. 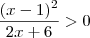 .
. 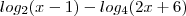 estar somente definido apenas para valores maiores que
estar somente definido apenas para valores maiores que  . Para quaisquer
. Para quaisquer 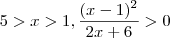 .
. 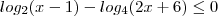 quando
quando ![x \in (1,5 ] x \in (1,5 ]](/latexrender/pictures/702e9e5cc81fcb8bbd65da2eecb5e4de.png) .
. 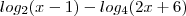 pertencentes a
pertencentes a ![(1, 5] (1, 5]](/latexrender/pictures/ef21171db41bbefe6ce048f5cac7fb49.png)
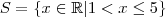 .
.
santhiago escreveu:Devemos determinar a solução paratal que
.
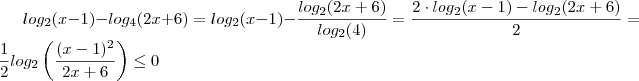
Caso 1 :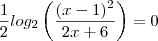
Como sabemos ,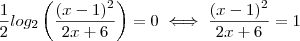
Que nos leva ,.
Neste caso único valor que satisfaz é.
Observe ,. Caso assumirmos
estamos entrando em contradição com a definição .
Caso 2 :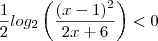
Agora temos que resolver ,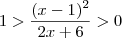
Mas como sabemos que ,quando
, ou seja
quando
.
Agora vamos resolver a outra inequação ,.
Perceba que ,estar somente definido apenas para valores maiores que
. Para quaisquer
.
Portanto através dos casos 1 e 2 , concluímos quequando
.
Faça o teste , atribua valores apertencentes a
![(1, 5] (1, 5]](/latexrender/pictures/ef21171db41bbefe6ce048f5cac7fb49.png)
Solução ,.
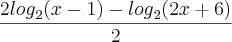
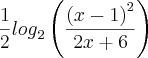

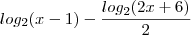 . Multiplicando o denominador e numerador por
. Multiplicando o denominador e numerador por  , não estamos alterando o resultado estamos multiplicando por
, não estamos alterando o resultado estamos multiplicando por  .
. 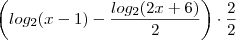 .
.  , fica ,
, fica , ![\left [ \left( log_2 (x-1 ) - \frac{log_2(2x +6)}{2}\right ) \cdot 2 \right] \cdot \frac{1}{2} \left [ \left( log_2 (x-1 ) - \frac{log_2(2x +6)}{2}\right ) \cdot 2 \right] \cdot \frac{1}{2}](/latexrender/pictures/f9c276448bfe8dc561e85dd6c5bedf8d.png)
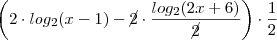
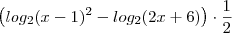
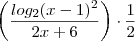

santhiago escreveu:OK. no problem !
Através da mudança de base , ficamos com ,. Multiplicando o denominador e numerador por
, não estamos alterando o resultado estamos multiplicando por
.
Veja como fica ,.
Aplicando a distributiva com o elemento, fica ,
![\left [ \left( log_2 (x-1 ) - \frac{log_2(2x +6)}{2}\right ) \cdot 2 \right] \cdot \frac{1}{2} \left [ \left( log_2 (x-1 ) - \frac{log_2(2x +6)}{2}\right ) \cdot 2 \right] \cdot \frac{1}{2}](/latexrender/pictures/f9c276448bfe8dc561e85dd6c5bedf8d.png)
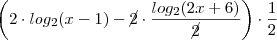
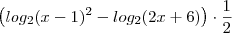
Ficou claro ?
Editado: Erro no texto .

santhiago escreveu:Devemos determinar a solução paratal que
.
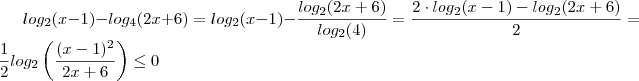
Caso 1 :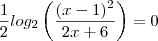
Como sabemos ,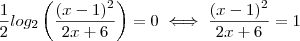
Que nos leva ,.
Neste caso único valor que satisfaz é.
Observe ,. Caso assumirmos
estamos entrando em contradição com a definição .
Caso 2 :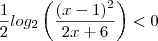
Agora temos que resolver ,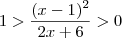
Mas como sabemos que ,quando
, ou seja
quando
.
Agora vamos resolver a outra inequação ,.
Perceba que ,estar somente definido apenas para valores maiores que
. Para quaisquer
.
Portanto através dos casos 1 e 2 , concluímos quequando
.
Faça o teste , atribua valores apertencentes a
![(1, 5] (1, 5]](/latexrender/pictures/ef21171db41bbefe6ce048f5cac7fb49.png)
Solução ,.

Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.