Um capital C, aplicado a juros compostos a uma taxa unitária i por período, produz,ao final de n períodos, o montante M, dado por
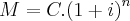 . Nessas condições, utilizando-se de log 2=0,30 e log 3=0,48, o capital de R$2000,00, aplicado a juro composto a taxa 20% ao ano, produzirá o montante de R$5000,00, ao final de um período de?
. Nessas condições, utilizando-se de log 2=0,30 e log 3=0,48, o capital de R$2000,00, aplicado a juro composto a taxa 20% ao ano, produzirá o montante de R$5000,00, ao final de um período de?Logaritmo não entra na minha cabeça e agora misturam juros e porcentagem? Me ajudem peloamor!


 . Somando
. Somando 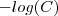 e mutiplicando ambos lados por
e mutiplicando ambos lados por 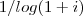 segue que ,
segue que , 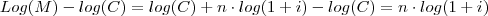
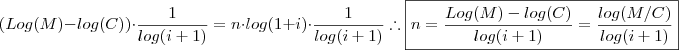




 , avisa que eu resolvo.
, avisa que eu resolvo.

