Um capital C, aplicado a juros compostos a uma taxa unitária i por período, produz,ao final de n períodos, o montante M, dado por
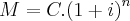 . Nessas condições, utilizando-se de log 2=0,30 e log 3=0,48, o capital de R$2000,00, aplicado a juro composto a taxa 20% ao ano, produzirá o montante de R$5000,00, ao final de um período de?
. Nessas condições, utilizando-se de log 2=0,30 e log 3=0,48, o capital de R$2000,00, aplicado a juro composto a taxa 20% ao ano, produzirá o montante de R$5000,00, ao final de um período de?Logaritmo não entra na minha cabeça e agora misturam juros e porcentagem? Me ajudem peloamor!


 . Somando
. Somando 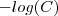 e mutiplicando ambos lados por
e mutiplicando ambos lados por 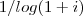 segue que ,
segue que , 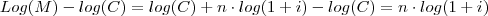
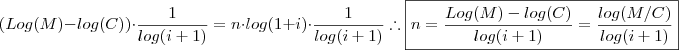



 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.