 por JU201015 » Seg Nov 12, 2012 21:05
por JU201015 » Seg Nov 12, 2012 21:05
(UFMG) Seja
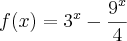
uma função real de variável real. O conjunto que contém todos os valores de x para os quais
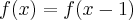
é?
Eu tentei igualando as duas mas não consegui =/ Como se faz?
-
JU201015
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Sáb Nov 10, 2012 00:01
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Seg Nov 12, 2012 21:16
por MarceloFantini » Seg Nov 12, 2012 21:16
De

temos que

. Multiplique tudo por

, daí

.
Em seguida, faça a substituição

. Portanto teremos

.
Termine.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por JU201015 » Ter Nov 13, 2012 09:59
por JU201015 » Ter Nov 13, 2012 09:59
MarceloFantini escreveu:De

temos que

. Multiplique tudo por

, daí

.
Em seguida, faça a substituição

. Portanto teremos

.
Termine.
Você colocou 36t - 9t²=12t -3t²
Mas não seria 36t - 9t²=12t -t² ?
Então fica 8t² + 24t = 0
E no fim, encontrei x=1.
-
JU201015
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Sáb Nov 10, 2012 00:01
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Ter Nov 13, 2012 10:03
por MarceloFantini » Ter Nov 13, 2012 10:03
Você está certa. Ao multiplicar

por 36 temos

.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por JU201015 » Ter Nov 13, 2012 19:15
por JU201015 » Ter Nov 13, 2012 19:15
JU201015 escreveu:MarceloFantini escreveu:De

temos que

. Multiplique tudo por

, daí

.
Em seguida, faça a substituição

. Portanto teremos

.
Termine.
Você colocou 36t - 9t²=12t -3t²
Mas não seria 36t - 9t²=12t -t² ?
Então fica 8t² + 24t = 0
E no fim, encontrei x=1.
Muitíssimo obrigada! ^^
-
JU201015
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Sáb Nov 10, 2012 00:01
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Questão POSCOMP 2011] Ajuda para interpretar questão
por hlustosa » Dom Jul 29, 2012 14:54
- 3 Respostas
- 12809 Exibições
- Última mensagem por hlustosa

Seg Jul 30, 2012 01:13
Funções
-
- Questão de P.A.
por mushthielv » Seg Ago 17, 2009 12:21
- 2 Respostas
- 10837 Exibições
- Última mensagem por Elcioschin

Ter Ago 18, 2009 08:54
Progressões
-
- QUESTÃO
por GABRIELA » Ter Set 08, 2009 16:32
- 2 Respostas
- 14583 Exibições
- Última mensagem por GABRIELA

Ter Set 08, 2009 21:21
Matrizes e Determinantes
-
- Questão da FCC
por wanderlymarques » Qua Nov 18, 2009 12:44
- 2 Respostas
- 4892 Exibições
- Última mensagem por wanderlymarques

Qui Nov 19, 2009 12:58
Cálculo: Limites, Derivadas e Integrais
-
- questão
por sirle ignes » Seg Mar 08, 2010 23:46
- 2 Respostas
- 4669 Exibições
- Última mensagem por sirle ignes

Ter Mar 09, 2010 17:32
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
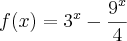 uma função real de variável real. O conjunto que contém todos os valores de x para os quais
uma função real de variável real. O conjunto que contém todos os valores de x para os quais 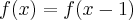 é?
é?
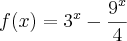 uma função real de variável real. O conjunto que contém todos os valores de x para os quais
uma função real de variável real. O conjunto que contém todos os valores de x para os quais 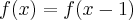 é?
é?
 temos que
temos que  . Multiplique tudo por
. Multiplique tudo por  , daí
, daí .
. . Portanto teremos
. Portanto teremos .
.

temos que
. Multiplique tudo por
, daí
.
. Portanto teremos
.


temos que
. Multiplique tudo por
, daí
.
. Portanto teremos
.

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
