 por Mayra Luna » Sáb Nov 10, 2012 15:05
por Mayra Luna » Sáb Nov 10, 2012 15:05
Na figura, ABC é um triângulo retângulo em que AB = 3 e AC =

.
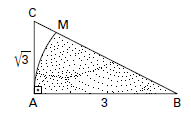
- triang.png (3.31 KiB) Exibido 1785 vezes
Se
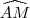
é um arco de circunferência de centro B, a área da região destacada é
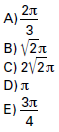
- resp.png (3.08 KiB) Exibido 1785 vezes
Resposta:
EChamei o ângulo
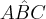
de

e resolvi:
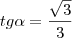
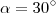
Aí calculei a área da circunferência
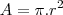
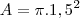
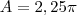
(Coloquei 1,5 pois acho que o lado AB é o diâmetro, está certo?)
Daí fiz a regra de três


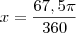
O que estou fazendo errado?
Grata desde já.
-
Mayra Luna
- Usuário Dedicado

-
- Mensagens: 46
- Registrado em: Dom Out 07, 2012 15:03
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por e8group » Sáb Nov 10, 2012 17:48
por e8group » Sáb Nov 10, 2012 17:48
Quase que você acertou , o raciocínio estar correto , mas o diâmetro é
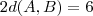
daí o raio será
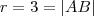
Fazendo a regra de três você chegara na resposta .
comente aí qualquer coisa .
Editado : Erro Com Latex
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Mayra Luna » Sáb Nov 10, 2012 18:01
por Mayra Luna » Sáb Nov 10, 2012 18:01
Ah, é verdade! Confundi o raio com o diâmetro.
Muito obrigada!!
-
Mayra Luna
- Usuário Dedicado

-
- Mensagens: 46
- Registrado em: Dom Out 07, 2012 15:03
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Geometria Plana - Triângulo] Triângulo Isós. e Bissetriz
por raimundoocjr » Qua Fev 22, 2012 09:41
- 3 Respostas
- 6607 Exibições
- Última mensagem por DanielFerreira

Sáb Fev 25, 2012 01:37
Geometria Plana
-
- Triangulo
por ginrj » Ter Abr 28, 2009 20:58
- 3 Respostas
- 3794 Exibições
- Última mensagem por ginrj

Sáb Mai 02, 2009 12:30
Geometria Plana
-
- Triângulo.
por Molina » Qua Mai 13, 2009 23:20
- 2 Respostas
- 2156 Exibições
- Última mensagem por Molina

Qui Mai 14, 2009 19:04
Geometria Plana
-
- Triângulo
por cristina » Seg Set 14, 2009 18:49
- 5 Respostas
- 3038 Exibições
- Última mensagem por Marcampucio

Ter Set 15, 2009 16:44
Trigonometria
-
- Triângulo
por Fogodc » Seg Abr 05, 2010 23:39
- 1 Respostas
- 1952 Exibições
- Última mensagem por Fogodc

Qua Abr 07, 2010 11:37
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 .
.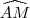 é um arco de circunferência de centro B, a área da região destacada é
é um arco de circunferência de centro B, a área da região destacada é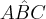 de
de  e resolvi:
e resolvi:
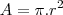
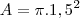
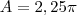


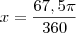


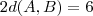 daí o raio será
daí o raio será 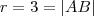


 .
.
 :
: