 por SCHOOLGIRL+T » Qua Nov 07, 2012 22:13
por SCHOOLGIRL+T » Qua Nov 07, 2012 22:13
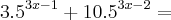
Me ajudem na simplificação desta equação que contém potenciação?
-
SCHOOLGIRL+T
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qua Nov 07, 2012 08:59
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Qua Nov 07, 2012 23:53
por MarceloFantini » Qua Nov 07, 2012 23:53
Note que
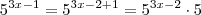
, daí
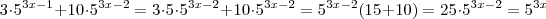
.
Estes exercícios são todos semelhantes. Se postar mais, espero mais esforço da sua parte.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por SCHOOLGIRL+T » Sex Nov 09, 2012 11:17
por SCHOOLGIRL+T » Sex Nov 09, 2012 11:17
MarceloFantini escreveu:Note que
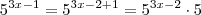
, daí
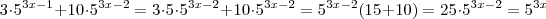
.
Estes exercícios são todos semelhantes. Se postar mais, espero mais esforço da sua parte.
Me desculpe, realmente postei mtos exercicios... =x
Mas é pq tenho mta dúvida e ainda não consigo aplicar as propriedades. E a cada vez que pergunto, eu aprendo um pouco, tipo, na sua resposta, eu aprendi que para somar as potências, podemos colocar um termo em evidência, certo? Então, mto obg! E, vou me esforçar mais, sim

-
SCHOOLGIRL+T
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qua Nov 07, 2012 08:59
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [potenciação] raiz cúbica com potenciação
por JKS » Qua Mar 06, 2013 17:41
- 2 Respostas
- 2292 Exibições
- Última mensagem por JKS

Qui Mar 14, 2013 16:43
Álgebra Linear
-
- [potenciação] módulo com potenciação
por JKS » Qua Mar 06, 2013 17:54
- 2 Respostas
- 1739 Exibições
- Última mensagem por JKS

Qui Mar 14, 2013 16:53
Equações
-
- POTENCIAÇÃO
por DANIELA » Sex Set 25, 2009 16:48
- 5 Respostas
- 3745 Exibições
- Última mensagem por DanielFerreira

Seg Set 28, 2009 10:20
Álgebra Elementar
-
- potenciação
por leandrofelip » Ter Fev 23, 2010 00:10
- 1 Respostas
- 2025 Exibições
- Última mensagem por Marcampucio

Ter Fev 23, 2010 12:56
Sistemas de Equações
-
- POTENCIACAO
por CaAtr » Ter Mar 09, 2010 20:23
- 3 Respostas
- 2294 Exibições
- Última mensagem por CaAtr

Ter Mar 09, 2010 22:17
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
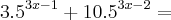

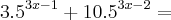

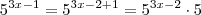 , daí
, daí 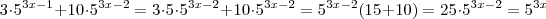 .
.

, daí
.

![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.