 por Netolucena » Ter Nov 06, 2012 15:17
por Netolucena » Ter Nov 06, 2012 15:17
ola pessoal agradeço as dicas que vocês todos nos passam, e estou aqui para pedir uma direção com a seguinte derivada , por conta da greve o professor não deu aula e está pedindo um trabalho com algumas coisas assim e não estamos com monitores dai estou meio que sem direção:
g(t) =

posso dizer que ela é

e fazer

ou é errado :s
se sim como deriva esse log ai ?
-
Netolucena
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Seg Fev 06, 2012 14:41
- Formação Escolar: GRADUAÇÃO
- Área/Curso: técnico em construção de edifícios
- Andamento: cursando
 por MarceloFantini » Ter Nov 06, 2012 15:35
por MarceloFantini » Ter Nov 06, 2012 15:35
Sim, está correto o que você escreveu. Se quiser deixar mais claro, escreva

.
Para derivar

use a regra da cadeia: as funções são

e
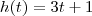
. Veja que

, e aplicando a regra da cadeia segue que
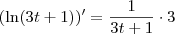
.
Não se esqueça que em

você tem uma regra do produto e depois uma regra da cadeia em
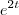
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Netolucena » Ter Nov 06, 2012 16:09
por Netolucena » Ter Nov 06, 2012 16:09
MarceloFantini escreveu:Sim, está correto o que você escreveu. Se quiser deixar mais claro, escreva

.
Para derivar

use a regra da cadeia: as funções são

e
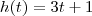
. Veja que

, e aplicando a regra da cadeia segue que
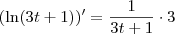
.
Não se esqueça que em

você tem uma regra do produto e depois uma regra da cadeia em
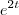
.
no caso como ln(3t+1) está elevado a -1 me dá

não seria ?

-
Netolucena
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Seg Fev 06, 2012 14:41
- Formação Escolar: GRADUAÇÃO
- Área/Curso: técnico em construção de edifícios
- Andamento: cursando
 por MarceloFantini » Ter Nov 06, 2012 16:33
por MarceloFantini » Ter Nov 06, 2012 16:33
Sim, é isto mesmo. Eu só mostrei como derivar

, mas falta a outra regra da cadeia.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por e8group » Ter Nov 06, 2012 16:34
por e8group » Ter Nov 06, 2012 16:34
Netolucena , para você check sua derivada , utilize o site wolfram alpha . Ele fornece o resultado e a solução completa . Por exemplo , digite lá : Derivative of ( ln( 3t +1) ) e pressione " ENTER " do seu teclado . Logo aparacerá o resultado , a direita do mesmo , há uma opção " step by step solution " , isto levará vc a solução completa .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Netolucena » Ter Nov 06, 2012 17:03
por Netolucena » Ter Nov 06, 2012 17:03
Obrigado por toda ajuda pessoal . . .
-
Netolucena
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Seg Fev 06, 2012 14:41
- Formação Escolar: GRADUAÇÃO
- Área/Curso: técnico em construção de edifícios
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada] Ajuda com calculo de derivada de função quociente
por alienpuke » Dom Out 25, 2015 15:31
- 1 Respostas
- 12556 Exibições
- Última mensagem por Cleyson007

Dom Out 25, 2015 16:47
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] Ajuda com calculo de derivada
por alienpuke » Sáb Out 24, 2015 15:45
- 2 Respostas
- 6988 Exibições
- Última mensagem por Cleyson007

Sáb Out 24, 2015 16:12
Cálculo: Limites, Derivadas e Integrais
-
- [calculo] derivada
por beel » Dom Set 25, 2011 13:04
- 2 Respostas
- 6893 Exibições
- Última mensagem por beel

Dom Set 25, 2011 16:22
Cálculo: Limites, Derivadas e Integrais
-
- [calculo] derivada de log
por beel » Sáb Out 15, 2011 22:42
- 4 Respostas
- 7458 Exibições
- Última mensagem por beel

Ter Out 18, 2011 13:16
Cálculo: Limites, Derivadas e Integrais
-
- [calculo] derivada de log 2
por beel » Dom Out 16, 2011 01:10
- 2 Respostas
- 6438 Exibições
- Última mensagem por Fabio Cabral

Ter Out 18, 2011 13:47
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.








 .
.  use a regra da cadeia: as funções são
use a regra da cadeia: as funções são  e
e 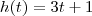 . Veja que
. Veja que  , e aplicando a regra da cadeia segue que
, e aplicando a regra da cadeia segue que 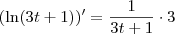 .
. você tem uma regra do produto e depois uma regra da cadeia em
você tem uma regra do produto e depois uma regra da cadeia em 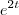 .
.

.
use a regra da cadeia: as funções são
e
. Veja que
, e aplicando a regra da cadeia segue que
.
você tem uma regra do produto e depois uma regra da cadeia em
.



 , mas falta a outra regra da cadeia.
, mas falta a outra regra da cadeia.



![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)