 por danielrodrigues » Seg Nov 05, 2012 23:49
por danielrodrigues » Seg Nov 05, 2012 23:49
Olá galera...eu novamente...tentei resolver essa inequação mas nao fui muito longe..
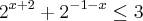
Fiz a separação dos numeros elevados e ficou assim
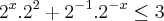
certo...dai substitui
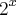
por y ficou assim:
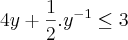
após o MMC
ficou:
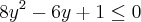
daí apliquei bhaskara e obtive:
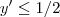
e

não sei se o procedimento está incorreto...só sei que cheguei até aí e não soube continuar...
se vcs puderem me ajudar...
Obrigado
-
danielrodrigues
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Seg Out 08, 2012 11:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Ambiental
- Andamento: cursando
 por MarceloFantini » Ter Nov 06, 2012 01:44
por MarceloFantini » Ter Nov 06, 2012 01:44
Até a inequação
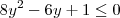
está OK. Agora calculando o discriminante temos
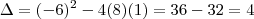
, daí
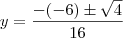
, que leva a
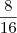
e
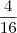
como raízes.
Como a parábola está virada de "boca para cima", ela será negativa entre as raízes. Logo teremos que, para que a inequação seja satisfeita, a variável está no intervalo
![\left[ \frac{4}{16}, \frac{8}{16} \right] \left[ \frac{4}{16}, \frac{8}{16} \right]](/latexrender/pictures/23a99d803326871f6f89ea7dfb615404.png)
, ou seja,
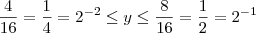
.
Voltando à variável original, temos que
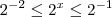
, de onde concluímos que
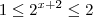
. Finalmente,

e portanto
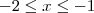
.
Editado pela última vez por
MarceloFantini em Ter Nov 06, 2012 13:44, em um total de 1 vez.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por danielrodrigues » Ter Nov 06, 2012 08:02
por danielrodrigues » Ter Nov 06, 2012 08:02
Cara só nao entendi pq vc nao resolveu a raiz de 4 na hora de calcular o y...vc simplesmente somou 6+4 e subtraiu 6-4 mas na verdade é raiz de 4=2
-
danielrodrigues
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Seg Out 08, 2012 11:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Ambiental
- Andamento: cursando
 por MarceloFantini » Ter Nov 06, 2012 13:44
por MarceloFantini » Ter Nov 06, 2012 13:44
Porque eu errei, você está certo. Já corrigi. Obrigado.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por danielrodrigues » Ter Nov 06, 2012 15:29
por danielrodrigues » Ter Nov 06, 2012 15:29
Imagina brother...eu quem agradeço!!
Agora entendi! Obrigado!
-
danielrodrigues
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Seg Out 08, 2012 11:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Ambiental
- Andamento: cursando
Voltar para Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Mais uma de sequência
por Molina » Dom Mai 03, 2009 06:07
- 4 Respostas
- 2918 Exibições
- Última mensagem por lucasguedes

Ter Jul 07, 2009 21:08
Desafios Difíceis
-
- MAIS UMA QUESTÃO DE G.A
por GABRIELA » Ter Set 29, 2009 18:57
- 3 Respostas
- 2547 Exibições
- Última mensagem por Elcioschin

Qua Set 30, 2009 20:54
Geometria Analítica
-
- Mais uma questão
por GABRIELA » Seg Dez 07, 2009 17:16
- 1 Respostas
- 2200 Exibições
- Última mensagem por Elcioschin

Seg Dez 07, 2009 19:23
Estatística
-
- Mais um desafio..
por victoreis1 » Seg Nov 22, 2010 21:26
- 3 Respostas
- 2534 Exibições
- Última mensagem por Molina

Seg Nov 22, 2010 23:54
Desafios Difíceis
-
- Mais uma questão de log
por my2009 » Qua Jan 26, 2011 11:41
- 1 Respostas
- 1405 Exibições
- Última mensagem por Molina

Qua Jan 26, 2011 15:21
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
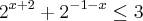
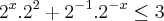
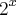 por y ficou assim:
por y ficou assim: 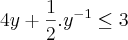
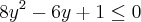
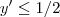 e
e 


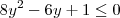 está OK. Agora calculando o discriminante temos
está OK. Agora calculando o discriminante temos 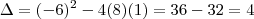 , daí
, daí 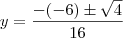 , que leva a
, que leva a 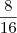 e
e 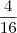 como raízes.
como raízes. ![\left[ \frac{4}{16}, \frac{8}{16} \right] \left[ \frac{4}{16}, \frac{8}{16} \right]](/latexrender/pictures/23a99d803326871f6f89ea7dfb615404.png) , ou seja,
, ou seja, 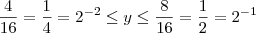 .
.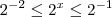 , de onde concluímos que
, de onde concluímos que 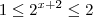 . Finalmente,
. Finalmente,  e portanto
e portanto 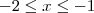 .
.


 .
.
 :
: