![{\sqrt[5]{1,1}}^{{x}^{2}+x+1} < 1 {\sqrt[5]{1,1}}^{{x}^{2}+x+1} < 1](/latexrender/pictures/e7ad57fa93e9a613c78ddc601751f568.png)
tentei resolver mas nao saiu nada...
Obrigado!!

![{\sqrt[5]{1,1}}^{{x}^{2}+x+1} < 1 {\sqrt[5]{1,1}}^{{x}^{2}+x+1} < 1](/latexrender/pictures/e7ad57fa93e9a613c78ddc601751f568.png)


![(\sqrt[5]{1,1})^{x^2 +x+1} < 1 (\sqrt[5]{1,1})^{x^2 +x+1} < 1](/latexrender/pictures/5053a6654d9f875c0de7bd6ce0276800.png)

![(\sqrt[5]{1,1})^{x^2 +x +1} (\sqrt[5]{1,1})^{x^2 +x +1}](/latexrender/pictures/a3710fd6f3aba45c5b9df3bb845ba0e1.png) seja menor que um devemos ter que o expoente é menor que zero, portanto
seja menor que um devemos ter que o expoente é menor que zero, portanto 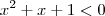 . Calcule o discriminante e conclua.
. Calcule o discriminante e conclua.




Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)