 por Bianca_R » Dom Nov 04, 2012 21:45
por Bianca_R » Dom Nov 04, 2012 21:45
Olá de novo,
Não consigo chegar na resposta que essa questão dá como certa.
A equação é:
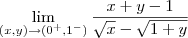
E a resposta é 0 (zero)
Estava tentando seguir o raciocínio de fazer
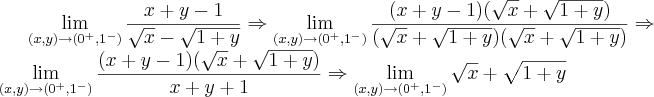
mas isso não dá zero no final. Dá algo perto de 1 não?
No que eu estou errando?
-
Bianca_R
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Dom Nov 04, 2012 17:03
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por e8group » Seg Nov 05, 2012 11:19
por e8group » Seg Nov 05, 2012 11:19
Sim , a resposta é zero . Perceba que o denominador fica diferente que zero , quando
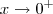
e
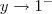
e também que ,
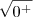
estar bem próximo do zero a direita e

à esquerda de
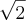
. Já no numerador isto não acontece . Em notação em termos de limites , tendo
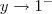
.Ficamos com ,
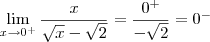
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite] Limite de funções reais de várias variáveis
por Bianca_R » Dom Nov 04, 2012 17:17
- 1 Respostas
- 4793 Exibições
- Última mensagem por MarceloFantini

Dom Nov 04, 2012 19:37
Cálculo: Limites, Derivadas e Integrais
-
- Limites duas variaveis
por Razoli » Qui Jul 03, 2014 23:22
- 2 Respostas
- 2595 Exibições
- Última mensagem por Razoli

Qui Jul 03, 2014 23:41
Cálculo: Limites, Derivadas e Integrais
-
- [LIMITES] Função de duas variáveis
por Sohrab » Ter Abr 23, 2013 03:18
- 7 Respostas
- 6779 Exibições
- Última mensagem por brunno10

Qua Mai 01, 2013 00:28
Cálculo: Limites, Derivadas e Integrais
-
- LIMITES função com duas variáveis, teo confronto
por inkz » Dom Nov 25, 2012 15:32
- 6 Respostas
- 9048 Exibições
- Última mensagem por e8group

Seg Nov 26, 2012 11:44
Cálculo: Limites, Derivadas e Integrais
-
- [LIMITES] - LIMITES DE DUAS VARIAVEIS
por Jol » Ter Fev 26, 2013 19:33
- 1 Respostas
- 1983 Exibições
- Última mensagem por young_jedi

Qua Fev 27, 2013 18:43
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
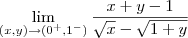
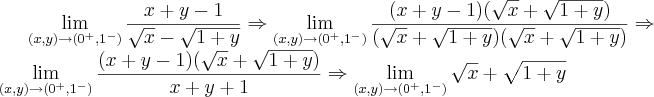

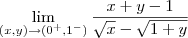
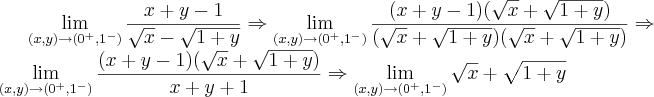

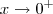 e
e 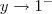 e também que ,
e também que , 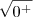 estar bem próximo do zero a direita e
estar bem próximo do zero a direita e  à esquerda de
à esquerda de 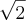 . Já no numerador isto não acontece . Em notação em termos de limites , tendo
. Já no numerador isto não acontece . Em notação em termos de limites , tendo 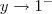 .Ficamos com ,
.Ficamos com , 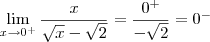


 .
.
 :
: