 por Sobreira » Sex Out 26, 2012 11:25
por Sobreira » Sex Out 26, 2012 11:25
Olá amigos,
Tenho que derivar esta função
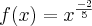
.
Derivando de forma direta, não encontro problema algum...
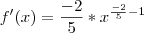
E resolvendo tudo no final encontro o resultado de:
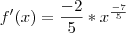
Agora eu não consigo entender ( e vejo que estou falhando com conceitos de matemática básica) se eu partir para resolver, antes de derivar, "ajeitando" a expressão.
Por exemplo:
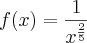
Gostaria que me descrevessem o desenrolar desta solução até a resposta final, pois tentei vários métodos e não chego ao final.
"The good thing about science is that it's true whether or not you believe in it."
-
Sobreira
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Sex Out 12, 2012 17:33
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por MarceloFantini » Sex Out 26, 2012 11:34
por MarceloFantini » Sex Out 26, 2012 11:34
Você tentou aplicar a regra do quociente? Segue que
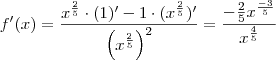
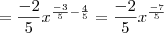
,
que era o resultado desejado.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Sobreira » Sex Out 26, 2012 14:55
por Sobreira » Sex Out 26, 2012 14:55
Beleza.
Eu estava tentando resolver e acabei ignorando as regras de derivação
Obrigado.

"The good thing about science is that it's true whether or not you believe in it."
-
Sobreira
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Sex Out 12, 2012 17:33
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Derivada com expoente fracionário.
por matematicouff » Seg Jun 18, 2012 02:39
- 1 Respostas
- 7340 Exibições
- Última mensagem por e8group

Seg Jun 18, 2012 17:48
Cálculo: Limites, Derivadas e Integrais
-
- Operações com radicais, potência de expoente fracionário...
por brunofelixinho » Ter Nov 12, 2013 20:45
- 0 Respostas
- 1772 Exibições
- Última mensagem por brunofelixinho

Ter Nov 12, 2013 20:45
Álgebra Elementar
-
- expressão com expoente negativo
por Andreza » Dom Jan 08, 2012 15:00
- 1 Respostas
- 2612 Exibições
- Última mensagem por Arkanus Darondra

Dom Jan 08, 2012 15:51
Álgebra Elementar
-
- Expressão com expoente decimal negativo
por cprado » Qua Dez 11, 2013 11:12
- 8 Respostas
- 4259 Exibições
- Última mensagem por Pessoa Estranha

Sáb Dez 14, 2013 18:02
Álgebra Elementar
-
- [Período Fracionário Exponencial] Fórmula - Urgente
por Scheuer » Sex Jun 15, 2012 17:46
- 1 Respostas
- 1981 Exibições
- Última mensagem por Russman

Sex Jun 15, 2012 19:04
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
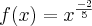 .
.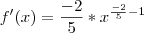
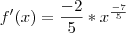
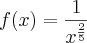


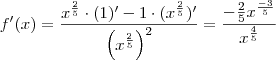
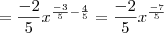 ,
,



 .
.



