 por Danilo » Seg Out 22, 2012 00:20
por Danilo » Seg Out 22, 2012 00:20
Encontre a equação de um plano que passa pelo ponto P = (2,1,0) e é perpendicular aos planos x+2y-3z+2 = 0 e 2x-y+4z=0.r
Então... o problema é que eu não consigo visualizar planos perpendiculares! Com reta tudo bem... mas com planos não. Sei da equação do plano, sei do vetor a..''normal'' ao plano... sei que a interseçao deles é uma reta... mas não consigo encaixar tudo isso para resolvero exercício. Grato a quem puder ajudar !
-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por MrJuniorFerr » Seg Out 22, 2012 00:59
por MrJuniorFerr » Seg Out 22, 2012 00:59
Para visualizar melhor planos perpendiculares, sugiro que tente analisar com 2/3 folhas de sulfite ou analise pelo livro: Geometria Analítica - Alfredo Steinbruch.
Para encontrar a equação do plano

, que no qual já foi dado um ponto pertencente a ele, você precisa achar o vetor normal a ele. Sabendo que há 2 planos perpendiculares a ele, n1(vetor normal ao plano1) e n2(vetor normal ao plano2), conclui-se que n1 e n2 são paralelos ao plano

, ou seja, fazendo n1 X n2 (produto vetorial), você descobre um vetor perpendicular a n1 e n2 e normal ao plano

, ou seja, você encontrou o vetor n do plano

, agora é só substituir em
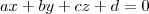
, achar o valor de d e você encontrou a equação geral do plano.
-

MrJuniorFerr
- Colaborador Voluntário

-
- Mensagens: 119
- Registrado em: Qui Set 20, 2012 16:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Alimentos
- Andamento: cursando
 por Danilo » Qua Out 24, 2012 20:26
por Danilo » Qua Out 24, 2012 20:26
Bom, eu entendi que para encontrar a equação de um plano basta um ponto e a normal deste plano. Sei que a interseção entre dois planos é uma reta. Eu não entendi por que a normal dos planos são paralelos ao plano que queremos encontrar. E também não entendi por que o produto vetorial das outras normais será a normal do plano que queremos encontrar... Grato!
-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por MarceloFantini » Qui Out 25, 2012 01:35
por MarceloFantini » Qui Out 25, 2012 01:35
Você precisa encontrar um vetor que seja normal ao vetor normal de cada um dos planos.
Uma boa forma de fazer isso é calcular o produto vetorial entre os vetores normais, pois ele garante que o vetor encontrado será ortogonal aos vetores dados.
Em símbolos, se
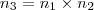
, então

e

. Em termos de produto interno, que é a caracterização usual, temos
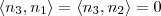
.
Encontrado este vetor, você já tem os valores
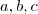
da equação geral do plano
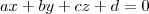
. Basta substituir o ponto dado e você encontrará
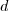
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Danilo » Qui Out 25, 2012 22:32
por Danilo » Qui Out 25, 2012 22:32
Obrigado!
-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Danilo » Qui Out 25, 2012 22:33
por Danilo » Qui Out 25, 2012 22:33
Obrigado!!!!
-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Danilo » Seg Out 29, 2012 16:05
por Danilo » Seg Out 29, 2012 16:05
Estou confuso com uma coisa: O que quer dizer quando um vetor é paralelo ao plano? Quer dizer que ele está ''dentro'' do plano? Eu estou com uma dificuldade imensa para desenhar/visualizar isso. Eu entendi os cálculos. Mas não vejo por que o cada normal é paralela a pi. Grato!
-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por MarceloFantini » Seg Out 29, 2012 18:03
por MarceloFantini » Seg Out 29, 2012 18:03
Se for paralelo ao plano pode estar dentro do plano, mas fora também. Pode ser uma reta ortogonal à normal do plano mas que não esteja contida no plano, isto é, não satisfaz a equação dada. De qualquer forma, em nenhum momento foi dito que algum vetor era paralelo a um plano.
Uma forma de visualizar isto é pegar uma caneta e colocar em cima de uma mesa. Agora suba a caneta mantendo a direção original. Você terá um vetor paralelo a um plano sem estar contido nele.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- PLANOS - PARALELISMO ENTRE PLANOS
por ubelima » Ter Jun 19, 2012 19:22
- 2 Respostas
- 5836 Exibições
- Última mensagem por ubelima

Qua Jun 20, 2012 01:01
Geometria Analítica
-
- [Interseção entre planos]
por sulafuly » Dom Mar 02, 2014 01:14
- 0 Respostas
- 2016 Exibições
- Última mensagem por sulafuly

Dom Mar 02, 2014 01:14
Geometria Analítica
-
- [GA] Ângulos entre planos
por Larissa28 » Dom Abr 05, 2015 10:03
- 3 Respostas
- 1827 Exibições
- Última mensagem por adauto martins

Sex Abr 10, 2015 11:29
Geometria Analítica
-
- Interseção entre planos
por marinasaboia » Sex Jan 08, 2016 14:44
- 1 Respostas
- 3236 Exibições
- Última mensagem por RuuKaasu

Sex Jan 15, 2016 21:52
Geometria Analítica
-
- medida angular entre planos
por -civil- » Sáb Jun 18, 2011 13:14
- 1 Respostas
- 2303 Exibições
- Última mensagem por LuizAquino

Sáb Jun 18, 2011 22:56
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 , que no qual já foi dado um ponto pertencente a ele, você precisa achar o vetor normal a ele. Sabendo que há 2 planos perpendiculares a ele, n1(vetor normal ao plano1) e n2(vetor normal ao plano2), conclui-se que n1 e n2 são paralelos ao plano
, que no qual já foi dado um ponto pertencente a ele, você precisa achar o vetor normal a ele. Sabendo que há 2 planos perpendiculares a ele, n1(vetor normal ao plano1) e n2(vetor normal ao plano2), conclui-se que n1 e n2 são paralelos ao plano 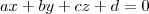 , achar o valor de d e você encontrou a equação geral do plano.
, achar o valor de d e você encontrou a equação geral do plano.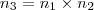 , então
, então  e
e  . Em termos de produto interno, que é a caracterização usual, temos
. Em termos de produto interno, que é a caracterização usual, temos 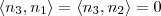 .
.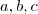 da equação geral do plano
da equação geral do plano 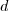 .
.
