 por cristian9192 » Sex Out 19, 2012 03:18
por cristian9192 » Sex Out 19, 2012 03:18
Já tentei de várias formas resolver essa integral definida, mais não tive sucesso em nem uma das tentativas, gostaria de alguma ajuda para resolver ela:
![\int_{-2}^{2}\sqrt[2]{16-y^2}-((y^2)/6)dy \int_{-2}^{2}\sqrt[2]{16-y^2}-((y^2)/6)dy](/latexrender/pictures/434d9085806ba5bc089e9c5af8d22932.png)
-
cristian9192
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Sex Out 19, 2012 02:13
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por young_jedi » Sex Out 19, 2012 11:27
por young_jedi » Sex Out 19, 2012 11:27
veja se sua integral é essa
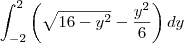
se não for da um toque
caso seja assim
voce pode separa em duas integrais
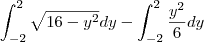
a segunda integral é tranquila pra resolver, mais quaquer duvida comente
a primeira, voce tem que fazer uma substituição trigonometrica
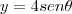
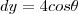
e temos que para y=2
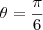
e para y=-2
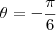
substituindo na integral
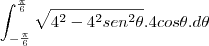
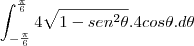
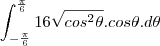
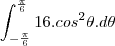
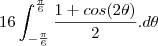
acredito que essa integral voce possa resolver tranquilo, mais qualquer duvida pergunte
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por cristian9192 » Sex Out 19, 2012 15:41
por cristian9192 » Sex Out 19, 2012 15:41
Obrigado, sua ajuda foi muito util, consegui terminar de resolver a integar.
-
cristian9192
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Sex Out 19, 2012 02:13
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Integral] Resolver Integral definida com trigonometria
por rodrigoboreli » Dom Set 07, 2014 01:02
- 1 Respostas
- 4211 Exibições
- Última mensagem por adauto martins

Sex Out 17, 2014 12:39
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo Integral] Integral Definida
por ARCS » Sáb Fev 02, 2013 21:37
- 2 Respostas
- 3532 Exibições
- Última mensagem por e8group

Sáb Fev 02, 2013 22:13
Cálculo: Limites, Derivadas e Integrais
-
- [integral] integral definida por partes
por gabriel feron » Seg Mar 11, 2013 00:48
- 2 Respostas
- 2942 Exibições
- Última mensagem por gabriel feron

Seg Mar 11, 2013 18:19
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Derivar integral definida
por troziinho » Ter Mar 31, 2015 20:26
- 0 Respostas
- 2412 Exibições
- Última mensagem por troziinho

Ter Mar 31, 2015 20:26
Cálculo: Limites, Derivadas e Integrais
-
- Integral definida
por exploit » Ter Set 07, 2010 19:17
- 4 Respostas
- 3487 Exibições
- Última mensagem por exploit

Qua Set 08, 2010 19:58
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\int_{-2}^{2}\sqrt[2]{16-y^2}-((y^2)/6)dy \int_{-2}^{2}\sqrt[2]{16-y^2}-((y^2)/6)dy](/latexrender/pictures/434d9085806ba5bc089e9c5af8d22932.png)


![\int_{-2}^{2}\sqrt[2]{16-y^2}-((y^2)/6)dy \int_{-2}^{2}\sqrt[2]{16-y^2}-((y^2)/6)dy](/latexrender/pictures/434d9085806ba5bc089e9c5af8d22932.png)

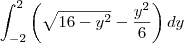
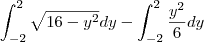
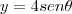
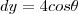
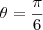
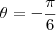
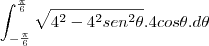
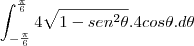
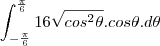
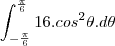
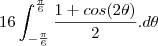



 .
.
 :
: