 por Ananda » Sex Mar 14, 2008 22:37
por Ananda » Sex Mar 14, 2008 22:37
Boa noite!
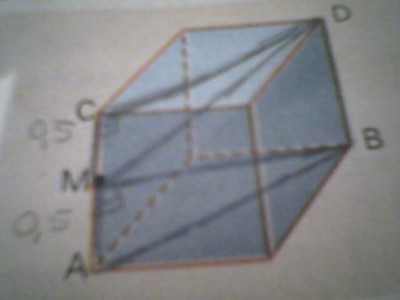
Eis o exercício: No cubo de aresta 1, considere as arestas AC e BC e o ponto médio M, de AC.
a) Determine o cosseno do ângulo BÂD.
b) Determine o cosseno do ângulo BMD. (M).
c) Qual dos ângulos BÂD ou BMd (M) é maior? Justifique.
Bom, o primeiro eu fiz assim:
a)cateto adjacente = AB = diagonal do quadrado = ![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
hipotenusa = AD = diagonal do cubo = ![\sqrt[]{3} \sqrt[]{3}](/latexrender/pictures/b84ccc0f808c82dca2d7b0f887c64445.png)
Logo, cosseno = ![\frac{\sqrt[]{2}}{\sqrt[]{3}}=\frac{\sqrt[]{6}}{3} \frac{\sqrt[]{2}}{\sqrt[]{3}}=\frac{\sqrt[]{6}}{3}](/latexrender/pictures/4c3b6ae55152e8082fbaadea7d3b677f.png)
Acredito que esteja certo já que a resposta é igual a do livro.
b) Estou em dúvida. Olho, olho para o desenho, mas não vejo saída. Em um momento, veio-me à mente considerar que os triângulos CDM e ABM são retângulos. Com isso, cheguei a ![\frac{\sqrt[]{7}}{3} \frac{\sqrt[]{7}}{3}](/latexrender/pictures/5d1cd480516ca0681b158beaab4e9af8.png) . Mas a resposta do livro é:
. Mas a resposta do livro é:  .
.
Vou colocar as contas que fiz:
2 =  +0,25
+0,25
MB=![\frac{\sqrt[]{7}}{2} \frac{\sqrt[]{7}}{2}](/latexrender/pictures/d3207d553aa6c1298bbc1fc4b39c881e.png)
 =2+0,25
=2+0,25
MD=1,5
cosseno = ![\frac{\sqrt[]{7}}{2}.\frac{2}{3}=\frac{\sqrt[]{7}}{3} \frac{\sqrt[]{7}}{2}.\frac{2}{3}=\frac{\sqrt[]{7}}{3}](/latexrender/pictures/8ced3459649b227e0647535a5c919190.png)
O que errei?
Bom, a letra c depende das respostas anteriores.
Grata desde já pela atenção!
Bom final de semana!
- Anexos
-
Ananda
-
Ananda
- Usuário Parceiro

-
- Mensagens: 55
- Registrado em: Sex Fev 22, 2008 19:37
- Área/Curso: Estudante
- Andamento: cursando
 por admin » Sex Mar 14, 2008 23:58
por admin » Sex Mar 14, 2008 23:58
Olá, Ananda!
O item (a) está certo sim.
O item (b) você errou por pouco. Há dois erros.
1) Os triângulos ABM e CDM são de fato retângulos, mas nos pontos A e C, respectivamente.
Refaça a conta para encontrar MB.
E como M é ponto médio de AC, segue que o triângulo BMD é isósceles.
Logo, MB = MD.
2) O triângulo BMD não é retângulo, ou seja, nele você não poderá aplicar a relação de cateto adjacente sobre hipotenusa.
Para encontrar o cosseno neste caso, você precisará da lei dos cossenos que relaciona dois lados adjacentes ao ângulo com o lado oposto.
Pense como uma extensão do teorema de Pitágoras para um triângulo qualquer.
Depois, com os dois valores dos cossenos, identifique e justifique qual ângulo é maior.
Não há apenas uma forma de justificar.
Se tiver dúvida na justificativa ou em "visualizar" qual ângulo é maior, comente comigo e discutimos.
Espero ter ajudado!
Bons estudos e bom final de semana!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por Ananda » Sáb Mar 15, 2008 13:21
por Ananda » Sáb Mar 15, 2008 13:21
Grata, Fábio!
Sobre a justificativa farei com relação ao fato de que quanto maior o ângulo, menor o cosseno.
Excelente final de semana!
Ananda
-
Ananda
- Usuário Parceiro

-
- Mensagens: 55
- Registrado em: Sex Fev 22, 2008 19:37
- Área/Curso: Estudante
- Andamento: cursando
 por admin » Sáb Mar 15, 2008 20:17
por admin » Sáb Mar 15, 2008 20:17
Olá.
Apenas cuidado com esta justificativa, não pode ser generalizada.
No intervalo
![[0, \pi] [0, \pi]](/latexrender/pictures/f74f8710fd31ce502365bc814a7fd3b6.png)
está correta, mas em
![[\pi, 2\pi] [\pi, 2\pi]](/latexrender/pictures/fd3a253ed973b49d40f54cf9fbf2a43b.png)
quanto maior o ângulo, maior o cosseno.
Até mais.
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por Ananda » Seg Mar 17, 2008 17:28
por Ananda » Seg Mar 17, 2008 17:28
Olá, Fábio!
Grata por me lembrar, saber eu sei, mas na hora de justificar tenho que tomar cuidado em deixar bem claro.
Mais uma vez grata!
Ananda
-
Ananda
- Usuário Parceiro

-
- Mensagens: 55
- Registrado em: Sex Fev 22, 2008 19:37
- Área/Curso: Estudante
- Andamento: cursando
Voltar para Geometria Espacial
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Cosseno
por karen » Ter Nov 27, 2012 13:17
- 1 Respostas
- 1569 Exibições
- Última mensagem por MarceloFantini

Ter Nov 27, 2012 19:24
Trigonometria
-
- Função Cosseno
por DanielFerreira » Qui Jul 30, 2009 17:41
- 1 Respostas
- 2877 Exibições
- Última mensagem por Felipe Schucman

Qui Jul 30, 2009 18:01
Trigonometria
-
- Seno e Cosseno de X??
por Leone de Paula » Ter Jul 13, 2010 00:28
- 1 Respostas
- 4664 Exibições
- Última mensagem por Tom

Ter Jul 13, 2010 00:43
Geometria Plana
-
- Lei do seno e cosseno
 por renataf » Sex Dez 03, 2010 11:06
por renataf » Sex Dez 03, 2010 11:06
- 7 Respostas
- 18829 Exibições
- Última mensagem por Lorettto

Sáb Dez 11, 2010 01:17
Trigonometria
-
- [LIMITE] cosseno
por beel » Ter Set 06, 2011 13:10
- 7 Respostas
- 7083 Exibições
- Última mensagem por beel

Sex Set 09, 2011 13:16
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
![\sqrt[]{3} \sqrt[]{3}](/latexrender/pictures/b84ccc0f808c82dca2d7b0f887c64445.png)
![\frac{\sqrt[]{2}}{\sqrt[]{3}}=\frac{\sqrt[]{6}}{3} \frac{\sqrt[]{2}}{\sqrt[]{3}}=\frac{\sqrt[]{6}}{3}](/latexrender/pictures/4c3b6ae55152e8082fbaadea7d3b677f.png)
![\frac{\sqrt[]{7}}{3} \frac{\sqrt[]{7}}{3}](/latexrender/pictures/5d1cd480516ca0681b158beaab4e9af8.png) . Mas a resposta do livro é:
. Mas a resposta do livro é:  .
. +0,25
+0,25![\frac{\sqrt[]{7}}{2} \frac{\sqrt[]{7}}{2}](/latexrender/pictures/d3207d553aa6c1298bbc1fc4b39c881e.png)
 =2+0,25
=2+0,25![\frac{\sqrt[]{7}}{2}.\frac{2}{3}=\frac{\sqrt[]{7}}{3} \frac{\sqrt[]{7}}{2}.\frac{2}{3}=\frac{\sqrt[]{7}}{3}](/latexrender/pictures/8ced3459649b227e0647535a5c919190.png)



![[0, \pi] [0, \pi]](/latexrender/pictures/f74f8710fd31ce502365bc814a7fd3b6.png) está correta, mas em
está correta, mas em ![[\pi, 2\pi] [\pi, 2\pi]](/latexrender/pictures/fd3a253ed973b49d40f54cf9fbf2a43b.png) quanto maior o ângulo, maior o cosseno.
quanto maior o ângulo, maior o cosseno.




