um segmento de reta e 
uma circunferência, para determinar o ponto inicial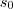 
e o final 
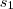do segmento de reta enrolada na circunferência, basta usar a relação 
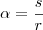, isso nada mais é do que a definição definição de ângulo.Agora o meu problema é o seguinte... eu gostaria de enrolar o mesmo segmento de reta numa elipse
e descobrir o ângulo 
que indicaria o início e o fim desse segmento enrolado na elipse... é possível fazer isso?Obg!
por ![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)