dúvida em ângulo

por **Rafael16** » Sex Out 05, 2012 13:07

: angulo2.gif (4.04 KiB) Exibido 1542 vezes

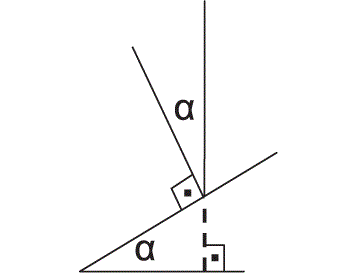
Olá pessoal, mão estou conseguindo entender como surge a soma de arcos sen e cos (sen(a+b) e cos(a+b)), devido a ângulos de lados perpendiculares serem iguais.
Não consigo entender isso, já estou ficando louco :-P

Por que os ângulos que têm lados perpendiculares são iguais? E como provar isso?

Valeu gente!

por **young_jedi** » Sex Out 05, 2012 13:40

: triangulos; demonstração.jpg (6.46 KiB) Exibido 1537 vezes

$b+90^o+90^o-\alpha=180^o$

$b=180^o-180^o+\alpha$

$b=\alpha$

por **Rafael16** » Sex Out 05, 2012 16:09

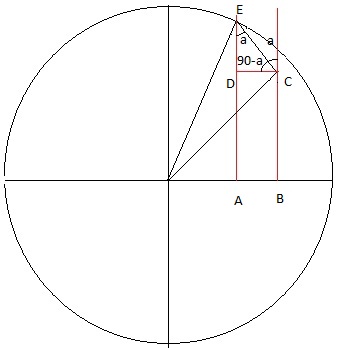
Obrigado young_jedi, finalmente entendi isso! Mas só não consigo entender o porque o ângulo 'a' são iguais na figura abaixo:

Não estou conseguindo aplicar o que você me explicou nessa circunferência trigonométrica.

por **young_jedi** » Sex Out 05, 2012 17:22

: circulo_trig; circulo_trig.jpg (18.81 KiB) Exibido 1523 vezes

prolongando o segmento BC tem se a mesma figura anterior

e levando em conta que o triangulo CDE é retangulo com angulo reto em D chega-se a conclusão do angulo a.

por **Rafael16** » Sex Out 05, 2012 17:58

Caramba você me salvou young_jedi, brigadão!!! :-D

dúvida em ângulo

dúvida em ângulo

dúvida em ângulo

Re: dúvida em ângulo

Re: dúvida em ângulo

Re: dúvida em ângulo

Re: dúvida em ângulo

Quem está online