Com relação à função quadrática f(x)+ -x²+2x-1, é fato que:
a) As suas raízes são iguais
Calcule o discriminante da função. Se for positivo as raízes são reais e distintas. Se negativo, complexas conjugadas e se nulo iguais e reais.b) O valor mínimo da função é positivo
c) O valor mínimo da função é negativo
O valor extremo é dado por 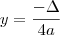 . Basta calculá-lo e observar o sinal.
. Basta calculá-lo e observar o sinal.d) A concavidade da parábola é positiva
Se o coeficiente do termo  for positivo então a concavidade é para cima. Se negativo, para baixo.
for positivo então a concavidade é para cima. Se negativo, para baixo.e) As raízes são simétricas em relação ao eixo y.
Somente se 
,


 é positivo, a concavidade da parabola é voltada para cima e quando o sinal é negativo a concavidade é voltada para baixo.
é positivo, a concavidade da parabola é voltada para cima e quando o sinal é negativo a concavidade é voltada para baixo.
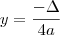 . Basta calculá-lo e observar o sinal.
. Basta calculá-lo e observar o sinal.



 .
.
 :
: