#Estude a função
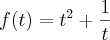 com relação à concavidade e pontos de inflexão.
com relação à concavidade e pontos de inflexão.Calculando a 1° derivada:
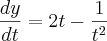
Calculando a 2° derivada:
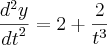
Para achar as raízes:
![2 + \frac{2}{{t}^{3}} = 0 \Leftrightarrow t = \sqrt[3]{-1} = -1 2 + \frac{2}{{t}^{3}} = 0 \Leftrightarrow t = \sqrt[3]{-1} = -1](/latexrender/pictures/deff47efd7c02adcb4ed33ca403394a6.png)
Então me ajude a partir daí por favor, to no caminho certo??

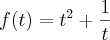 com relação à concavidade e pontos de inflexão.
com relação à concavidade e pontos de inflexão.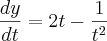
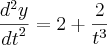
![2 + \frac{2}{{t}^{3}} = 0 \Leftrightarrow t = \sqrt[3]{-1} = -1 2 + \frac{2}{{t}^{3}} = 0 \Leftrightarrow t = \sqrt[3]{-1} = -1](/latexrender/pictures/deff47efd7c02adcb4ed33ca403394a6.png)



 , -1[ e ]0,+
, -1[ e ]0,+ [
[

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)