 por Alerecife » Ter Set 18, 2012 12:27
por Alerecife » Ter Set 18, 2012 12:27
Olá pessoal tudo bem!
- Alguém poderia me ajuda na solução desse problema abaixo:
Uma rodovia representada pelo plano

, sofre um tremor, havendo um rebaixamento da rodovia representado pelo plano

.
Como posso calcular o quanto foi o rebaixamento dessa rodovia após o tremor?
PELA ATENÇÃO OBRIGADO!
-
Alerecife
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Ter Set 04, 2012 12:02
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura
- Andamento: cursando
 por young_jedi » Ter Set 18, 2012 12:57
por young_jedi » Ter Set 18, 2012 12:57
primeiro voce deve encontrar o vetor N que é normal aos dois planos
depois voce encontrar um ponto P que pertença a um plano e um ponto Q que pertença a outro plano
então voce encontra o veto PQ, sendo que a projeção do mesmo sobre o vetor N dara a distancia entre os planos
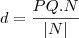
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Alerecife » Ter Set 18, 2012 21:16
por Alerecife » Ter Set 18, 2012 21:16
Obrigado!!
- vou calcular a normal para os dois planos....
-
Alerecife
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Ter Set 04, 2012 12:02
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 , sofre um tremor, havendo um rebaixamento da rodovia representado pelo plano
, sofre um tremor, havendo um rebaixamento da rodovia representado pelo plano  .
.

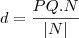


 .
.



