 por Felipe santos santos » Sex Set 07, 2012 16:43
por Felipe santos santos » Sex Set 07, 2012 16:43
Outras dúvidas em conjuntos :
Existe algum método para resolver questões onde é dado o numero de elementos do conjunto, como por exemplo na questão :
Denotemos por n(X) o número de elementos
de um conjunto finito X. Sejam A, B e C conjuntos
tais que n(A U B) = 8, n(A U C) = 9,
n(B U C) = 10, n(A U B U C) = 11 e
n(A ? B ? C) = 2. Então, n(A) + n(B) + n(C)
é igual a :
a) 11. b) 14. c) 15. d) 18. e) 25.
Eu não estou conseguindo desenvolver questões desse tipo .
Agradeço desde já.
-
Felipe santos santos
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Ter Set 04, 2012 08:06
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Pré-vest
- Andamento: cursando
 por MarceloFantini » Sex Set 07, 2012 17:54
por MarceloFantini » Sex Set 07, 2012 17:54
É interessante lembrar da relação
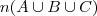
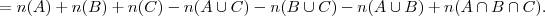
Usando isto, basta isolar
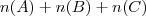
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Felipe santos santos » Sex Set 07, 2012 18:05
por Felipe santos santos » Sex Set 07, 2012 18:05
MarceloFantini escreveu:É interessante lembrar da relação
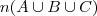
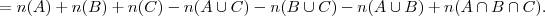
Usando isto, basta isolar
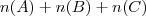
.
Vlw cara , ajudo muito .
-
Felipe santos santos
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Ter Set 04, 2012 08:06
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Pré-vest
- Andamento: cursando
Voltar para Conjuntos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Conjuntos] Confusão em teoria dos conjuntos numa questão.
 por Debora Bruna » Seg Jan 11, 2016 17:44
por Debora Bruna » Seg Jan 11, 2016 17:44
- 1 Respostas
- 8841 Exibições
- Última mensagem por DanielFerreira

Sáb Jan 23, 2016 16:44
Conjuntos
-
- [Conjuntos] Dúvida sobre conjuntos vazios
por ALPC » Qui Set 18, 2014 18:28
- 5 Respostas
- 6420 Exibições
- Última mensagem por adauto martins

Seg Set 22, 2014 15:44
Conjuntos
-
- [conjuntos]numeros racionais e conjuntos
por fenixxx » Ter Fev 28, 2012 21:35
- 3 Respostas
- 4730 Exibições
- Última mensagem por DanielFerreira

Sex Mar 02, 2012 00:04
Álgebra Elementar
-
- [Conjuntos] Problema de conjuntos com porcentagem
por Tibes » Qui Jan 31, 2013 14:29
- 1 Respostas
- 7958 Exibições
- Última mensagem por young_jedi

Sex Fev 01, 2013 12:39
Conjuntos
-
- [Conjuntos] Conjuntos e geometria plana
por bencz » Dom Mar 03, 2013 12:58
- 3 Respostas
- 11206 Exibições
- Última mensagem por maison_souza

Sex Nov 14, 2014 13:15
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


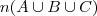
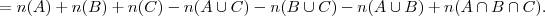
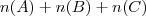 .
.

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.