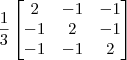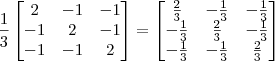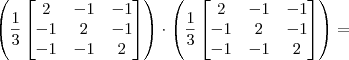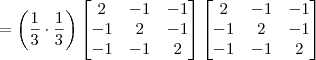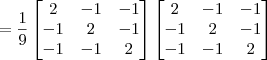por cramos_err » Sex Ago 31, 2012 19:49
por cramos_err » Sex Ago 31, 2012 19:49
uma matriz quadrada é chamada de idempotentes se a²=a. Verifique que a matriz 1/3 |2 -1 -1|
|-1 2 -1|
|-1 -1 2|
é idempotente.
-
cramos_err
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Ago 31, 2012 19:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por LuizAquino » Sex Ago 31, 2012 19:58
por LuizAquino » Sex Ago 31, 2012 19:58
cramos_err escreveu:uma matriz quadrada é chamada de idempotentes se a²=a. Verifique que a matriz 1/3 |2 -1 -1|
|-1 2 -1|
|-1 -1 2|
é idempotente.
Qual foi exatamente a sua dúvida? Basta calcular o produto A*A e conferir se isto é igual a própria matriz A.
ObservaçãoPor favor, procure usar o
LaTeX para digitar as notações de forma adequada.
Por exemplo, para digitar a matriz desejada basta usar o código:
- Código: Selecionar todos
[tex]
\frac{1}{3}\begin{bmatrix}
2 & - 1 & -1 \\
-1 & 2 & -1\\
-1 & -1 & 2
\end{bmatrix}
[/tex]
O resultado desse código será:
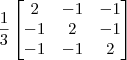
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por cramos_err » Sex Ago 31, 2012 20:08
por cramos_err » Sex Ago 31, 2012 20:08
LuizAquino escreveu:cramos_err escreveu:uma matriz quadrada é chamada de idempotentes se a²=a. Verifique que a matriz 1/3 |2 -1 -1|
|-1 2 -1|
|-1 -1 2|
é idempotente.
Qual foi exatamente a sua dúvida? Basta calcular o produto A*A e conferir se isto é igual a própria matriz A.
ObservaçãoPor favor, procure usar o
LaTeX para digitar as notações de forma adequada.
Por exemplo, para digitar a matriz desejada basta usar o código:
- Código: Selecionar todos
[tex]
\frac{1}{3}\begin{bmatrix}
2 & - 1 & -1 \\
-1 & 2 & -1\\
-1 & -1 & 2
\end{bmatrix}
[/tex]
O resultado desse código será:
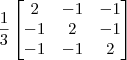
Me descupe, pois sou novo no forum.
Mais a minha dúvida é pq 1/3, tem como vc fazer esse execício, para eu ver como fica, é apenas um exemplo.
Agradeço desde já.
-
cramos_err
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Ago 31, 2012 19:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por LuizAquino » Sex Ago 31, 2012 20:46
por LuizAquino » Sex Ago 31, 2012 20:46
cramos_err escreveu:Mais a minha dúvida é pq 1/3, tem como vc fazer esse execício, para eu ver como fica, é apenas um exemplo.
Ao invés de "lhe dar o peixe", eu vou lhe "ensinar a pescar". Eu mostrarei o caminho e você tenta seguir. Se você não conseguir terminar, então poste aqui até onde conseguiu avançar.
Note que esse 1/3 é apenas um escalar multiplicando toda a matriz. Lembre-se que multiplicar um escalar por uma matriz é apenas realizar a seguinte operação:
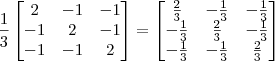
Agora bastaria calcular o produto:

Se o resultado desse produto for igual a matriz inicial, então a matriz é idempotente.
Mas ao invés de fazer por esse caminho, o mais interessante seria efetuar a seguinte arrumação:
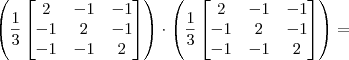
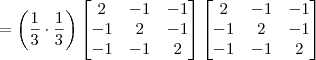
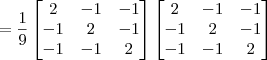
Agora basta calcular o produto entre as matrizes e comparar com a inicial. Note que esse produto é bem mais simples do que aquele entre as matrizes anteriores.
Tente continuar a partir daí.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [MATRIZ] Como acho o determinante dessa matriz
por LAZAROTTI » Qui Mai 03, 2012 00:38
- 4 Respostas
- 7179 Exibições
- Última mensagem por Russman

Qui Mai 03, 2012 01:56
Matrizes e Determinantes
-
- [Matriz]- inversa de uma matriz
por Ana_Rodrigues » Seg Mar 26, 2012 08:54
- 2 Respostas
- 3580 Exibições
- Última mensagem por Ana_Rodrigues

Seg Mar 26, 2012 18:05
Matrizes e Determinantes
-
- [MATRIZ]Determinante da Matriz 4x4
por LAZAROTTI » Qui Mai 03, 2012 22:33
- 1 Respostas
- 6730 Exibições
- Última mensagem por LuizAquino

Sex Mai 11, 2012 08:00
Matrizes e Determinantes
-
- [Matriz] Matriz com potencias
por rochadapesada » Dom Abr 07, 2013 20:29
- 3 Respostas
- 4705 Exibições
- Última mensagem por DanielFerreira

Seg Abr 08, 2013 17:32
Matrizes e Determinantes
-
- matriz
por Barbara » Ter Ago 18, 2009 15:26
- 4 Respostas
- 4817 Exibições
- Última mensagem por Molina

Qui Ago 20, 2009 18:11
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.