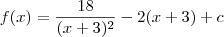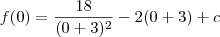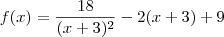por sueliasuki » Qui Ago 23, 2012 18:20
por sueliasuki » Qui Ago 23, 2012 18:20
Considere uma função f(x) tal que f(0) = 5 e df/dx =-36 /(x+3)3 - 2. Encontre a função f(x) e calcule o valor de f(3).
-
sueliasuki
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qui Ago 23, 2012 18:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia civil
- Andamento: cursando
 por LuizAquino » Qui Ago 23, 2012 18:54
por LuizAquino » Qui Ago 23, 2012 18:54
sueliasuki escreveu:Considere uma função f(x) tal que f(0) = 5 e df/dx =-36 /(x+3)3 - 2. Encontre a função f(x) e calcule o valor de f(3).
Por favor, procure usar o
LaTeX para inserir as notações de forma adequada.
Qual é a expressão original para df/dx? Por acaso seria
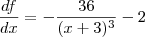
? Ou seria outra coisa?
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por sueliasuki » Qui Ago 23, 2012 19:44
por sueliasuki » Qui Ago 23, 2012 19:44
Correto, é desse jeito. Não consegui a configuração certa.
Aguardo sua ajuda.
-
sueliasuki
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qui Ago 23, 2012 18:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia civil
- Andamento: cursando
 por LuizAquino » Sex Ago 24, 2012 08:06
por LuizAquino » Sex Ago 24, 2012 08:06
sueliasuki escreveu:Correto, é desse jeito. Não consegui a configuração certa.
Primeiro note que
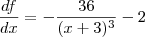
é o mesmo que
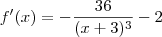
.
Calculando a integral de ambos os membros da equação, temos que:
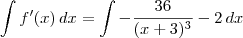
A integral no primeiro membro é simples. Basta aplicar o Teorema Fundamental do Cálculo:
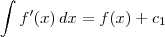
Já a integral no segundo membro, podemos resolver usando a substituição u = x + 3 (tente fazer). Vamos obter:
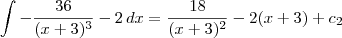
Desse modo, temos que:
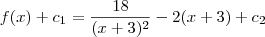
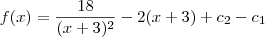
Como

e

são constantes, temos que a subtração

também é uma constante. Vamos chamar o resultado dessa subtração de c. Desse modo, ficamos com:
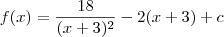
Agora basta usar o fato de que f(0) = 5 para determinar o valor da constante c:
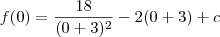


Sendo assim, temos que:
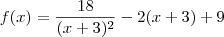
Agora calcule f(3) para concluir o exercício.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- ajuda
por Daiane kelly » Seg Mar 24, 2008 22:38
- 4 Respostas
- 6390 Exibições
- Última mensagem por Cleyson007

Ter Mai 12, 2009 17:43
Matrizes e Determinantes
-
- Ajuda
por Umbus » Sáb Out 18, 2008 14:12
- 2 Respostas
- 3677 Exibições
- Última mensagem por lopes

Sáb Jun 20, 2009 15:51
Álgebra Linear
-
- Ajuda.
por VanessaFontela » Qui Dez 04, 2008 10:32
- 0 Respostas
- 2897 Exibições
- Última mensagem por VanessaFontela

Qui Dez 04, 2008 10:32
Matemática Financeira
-
- Ajuda!!!
por GABRIELA » Seg Set 21, 2009 17:28
- 1 Respostas
- 2289 Exibições
- Última mensagem por Molina

Seg Set 21, 2009 19:56
Sistemas de Equações
-
- Ajuda!!!!!!
por GABRIELA » Ter Set 22, 2009 16:35
- 6 Respostas
- 4429 Exibições
- Última mensagem por GABRIELA

Qui Set 24, 2009 16:29
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



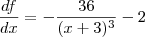 ? Ou seria outra coisa?
? Ou seria outra coisa?

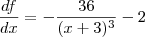 é o mesmo que
é o mesmo que 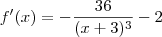 .
.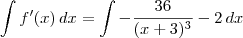
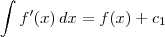
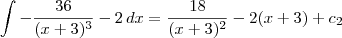
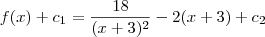
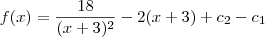
 e
e  são constantes, temos que a subtração
são constantes, temos que a subtração  também é uma constante. Vamos chamar o resultado dessa subtração de c. Desse modo, ficamos com:
também é uma constante. Vamos chamar o resultado dessa subtração de c. Desse modo, ficamos com: