


sueliasuki escreveu:Considere uma função f(x) tal que f(0) = 5 e df/dx =-36 /(x+3)3 - 2. Encontre a função f(x) e calcule o valor de f(3).
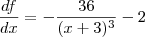 ? Ou seria outra coisa?
? Ou seria outra coisa?

sueliasuki escreveu:Correto, é desse jeito. Não consegui a configuração certa.
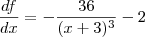 é o mesmo que
é o mesmo que 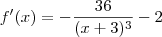 .
.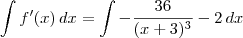
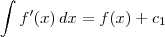
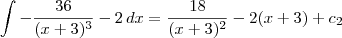
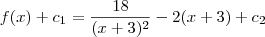
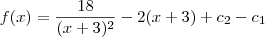
 e
e  são constantes, temos que a subtração
são constantes, temos que a subtração  também é uma constante. Vamos chamar o resultado dessa subtração de c. Desse modo, ficamos com:
também é uma constante. Vamos chamar o resultado dessa subtração de c. Desse modo, ficamos com: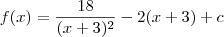
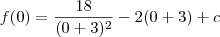


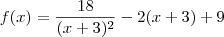

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante