Olá pessoal, gostaria muito da ajuda de vocês em uma questão da VUNESP. O enunciado diz o seguinte:
Uma escada tem 25 degraus iguais. A altura h de cada degrau está para a largura l assim como 2 está para 5. O desnível entre o quinto degrau e o pé da escada A é 1 metro. Qual a distância entre o pé da escada A e o topo da escada B?
Primeiramente tentei fazer uma semelhança de triângulos entre os primeiros 5 degraus com a altura 100 (por ser 1 metro) e um degrau de altura 2 e base 5. Com o resultado obtido que foi de 250 fiz o teorema de Pitágora para achar a hipotenusa. Achando está multipliquei por 25. O resultado deu um absurdo!! 135 metros entre A e B. Mas na verdade o resultado correto é 13m. Gostaria de saber o que fiz de errado e como chegar ao resultado correto!
Obrigada ^^



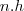 , onde
, onde  é o número de degraus e
é o número de degraus e  a altura particular de cada um.
a altura particular de cada um. , pois temos de descontar um degrau que não contribui!
, pois temos de descontar um degrau que não contribui!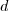 a distãncia do pé ao topo temos
a distãncia do pé ao topo temos
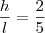 e o desnível do quinto degrau é um metro, isto é,
e o desnível do quinto degrau é um metro, isto é, 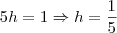 , então
, então 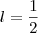 .
. .
.
 .
.
 :
: