saudações!
1) Não estou entendendo como interpretar corretamente a notação da função derivada.
Poisbem, considerando as seguintes premissas:
f'(x) = d/dx(x) = [f(x+h)-f(x)]/h
o que é colocado no "(x)" deve ser colocado na definição de derivada também...
logicamente me parece um pouco estranho... porque deriva-se uma função (f(x) = x²-3x+2, por ex.), então a função f(x) é que deveria ir dentro da diferenciação: "f'(f(x))"... não é assim que ocorre mas é compreensível... o que ocrorre na verdade são umas transformações com a função f(x) e resultado será nomeada de f'(x). ok...
Mas nas regras operatórias básicas de diferenciação tem-se que: [f(x)+g(x)]' = f'(x)+g'(x)... o que me é ainda mais logicamente estranho, porque em [f(x)+g(x)]', duas funções, f(x) e g(x), estão sendo derivadas pela notação [...]'. Trocando de notação para, vamos ver... f'(...) não, muito estranho, então para d/dx(...), parece razoável, afinal as duas funções estão sendo derivadas!
vejamos:
d/dx[f(x)+g(x)] = d/dx[f(x)]+d/dx[g(x)]
parece logicamente melhor... mas, f'(x) = d/dx(x), então é só trocar d/dx(x) por f'(x) que fica estranho de novo...
enfim... não consegui entender o significa de (...)'
2) Na notação f'(x), o que se coloca no x é o que vai pra definição de derivada no outro lado da igualdade, certo. Mas na derivada da soma [f(x)+g(x)]' o que é substituido na definição [f(x+h)-f(x)]/h não é o x, como de costume, mas sim o f e o g! Ficando então: {[f(x+h)+g(x+h)]-[f(x)+g(x)]}/2. Tomando a parte final da equação anterior [f(x)+g(x)], ela é a que mais se aproxima da derivada da soma [f(x)+g(x)]'. Mas na definição original, esta parte final é -[f(x)]. Portanto, é como se [f(x)+g(x)] fosse igual a [f(x)], e por isso foi substituida na parte final da definição e nela toda.
O FATO é que se deriva [f(x)+g(x)]' e na definição de derivada, o que aparece no lugar de f(x) é o f(x) somado com o g(x)...
OU SEJA, houve uma substituição de f para g+f... mas em funções APENAS substituimos o (x)... a não ser que no lugar do (x) apareça uma coisa do tipo (f(x)+g(x))... isto lebra d/dx( f(x)+g(x) ) que lembra f'( f(x)+g(x) )...
enfim, tudo isso me lembra meus "professores doutores" "ensinando" trinometria sem explicar o significado das funções no círculo trigonométrico... (e eu ainda tenho mais dúvidas com notações do tipo: d/dx(u+v) = d/dx(u) + d/dx(v)...)
é um textin grandin... kkkkk... mas não passa de definições e interpretações...
obrigado a quem me ajudar!
José


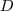 esta operação,
esta operação, 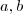 números reais quaisquer e
números reais quaisquer e  funções da variável x, temos
funções da variável x, temos![D[af(x)+bg(x)] = aD[f(x)] + bD[g(x)] D[af(x)+bg(x)] = aD[f(x)] + bD[g(x)]](/latexrender/pictures/6e66579af87e88816b075f2688076660.png) .
.![D[3x+6x^2] = 3 D[x] + 6D[x^2] D[3x+6x^2] = 3 D[x] + 6D[x^2]](/latexrender/pictures/59102be44e09aad778562bc84829c720.png) .
.![D[f(x)]=\lim_{h\rightarrow 0}\frac{f(x+h)-f(x)}{h} D[f(x)]=\lim_{h\rightarrow 0}\frac{f(x+h)-f(x)}{h}](/latexrender/pictures/a404bb861acd1dac8b8b254ce0e3fe3a.png) .
.![D[f(x)] = \frac{\mathrm{d} }{\mathrm{d} x}f(x) = f'(x) D[f(x)] = \frac{\mathrm{d} }{\mathrm{d} x}f(x) = f'(x)](/latexrender/pictures/1faea9b840f090980d8a9ea2fb5664f0.png) é apenas uma convensão de NOTAÇÃO.
é apenas uma convensão de NOTAÇÃO.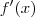 é apenas uma maneira mais concisa de escrever
é apenas uma maneira mais concisa de escrever ![[f(x)]' [f(x)]'](/latexrender/pictures/0fc35a5f83c3056e47c2b6d736d5b48b.png) , significando a derivada da função
, significando a derivada da função  . Ou seja,
. Ou seja, ![\frac{\textrm{d} ...}{\textrm{d}x} = [...]' \frac{\textrm{d} ...}{\textrm{d}x} = [...]'](/latexrender/pictures/36fa3663a3b6cfa6bb21da53c4e5327e.png) . Você não está sabendo ligar com a notação: note que se escrevemos
. Você não está sabendo ligar com a notação: note que se escrevemos  ou
ou  . Também não sei o que quer dizer com
. Também não sei o que quer dizer com  , por favor use LaTeX para os símbolos, facilitando o entendimento de todos.
, por favor use LaTeX para os símbolos, facilitando o entendimento de todos.![f'(x) = [f(x)]' f'(x) = [f(x)]'](/latexrender/pictures/6ec974da663ed67ea2eb4447206604ca.png) . Portanto, se
. Portanto, se  , então
, então ![[h(x)]' = [f(x)+g(x)]' [h(x)]' = [f(x)+g(x)]'](/latexrender/pictures/5979653e65ed291391a744c7f90cd10c.png) . Não é a função
. Não é a função 


 então , para lembrar dessa dependência, escrevemos
então , para lembrar dessa dependência, escrevemos  e denotamos sua derivada como
e denotamos sua derivada como  não pode seguir essa convenção uma vez que ela possui DUAS variáveis. Assim, somos obrigados a expressar suas derivadas respectivamente a cada variável pela notação conhecida como de Leibniz:
não pode seguir essa convenção uma vez que ela possui DUAS variáveis. Assim, somos obrigados a expressar suas derivadas respectivamente a cada variável pela notação conhecida como de Leibniz:  ou
ou  , onde nessa última a notação quer significar que a derivação é uma operação sendo aplicada na função e não um quociente como na primeira.
, onde nessa última a notação quer significar que a derivação é uma operação sendo aplicada na função e não um quociente como na primeira.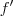 ,
,