 por Danilo » Qua Jul 18, 2012 23:28
por Danilo » Qua Jul 18, 2012 23:28
Provar que
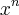
-
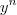
para n inteiro positivo. Bom, eu ''peguei'a prova'' em um livro, mas eu não compreendi alguns artifícios algébricos utilizados pelo autor do livro, por isto estou aqui, para que alguem me ajude a entender. Primeiro vou colocar toda a resolução e depois vou dizer o que não entendi.
Vamos provar que Provar que
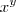
-
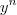
= (x - y) (
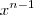
+
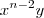
+....+
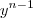
.
Inicialmente, vamos mostrar que se a

1,
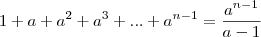
De fato,
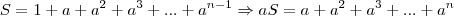
Subtraindo as duas equações anteriores,
aS - S =


(a-1) S =


S=
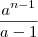
Agora fazendo
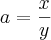
na expressão
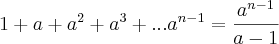
,
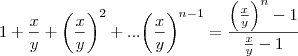

![\left(\frac{x}{y}-1 \right)\left[1+\frac{x}{y}+{\left(\frac{x}{y} \right)}^{2}+...+{\left(\frac{x}{y} \right)}^{n-1}={\left(\frac{x}{y} \right)}^{n} \right]={\left(\frac{x}{y}
\right)}^{n}-1\Rightarrow \left(\frac{x}{y}-1 \right)\left[1+\frac{x}{y}+{\left(\frac{x}{y} \right)}^{2}+...+{\left(\frac{x}{y} \right)}^{n-1}={\left(\frac{x}{y} \right)}^{n} \right]={\left(\frac{x}{y}
\right)}^{n}-1\Rightarrow](/latexrender/pictures/b55b363a766543b698e7d099cd436722.png)
![\left(\frac{x}{y}-1 \right)\left[1+\frac{x}{y}+{\left(\frac{x}{y} \right)}^{2}+...+{\left(\frac{x}{y} \right)}^{n-1} \right]= \frac{{x}^{n}-{y}^{n}}{{y}^{n}} \left(\frac{x}{y}-1 \right)\left[1+\frac{x}{y}+{\left(\frac{x}{y} \right)}^{2}+...+{\left(\frac{x}{y} \right)}^{n-1} \right]= \frac{{x}^{n}-{y}^{n}}{{y}^{n}}](/latexrender/pictures/3aaecbc7bc35c0a88573bc0df4c232bb.png)
![{y}^{n}\left(\frac{x-y}{y} \right)\left[1+\frac{x}{y}+{\left(\frac{x}{y} \right)}^{2}+...+{\left(\frac{x}{y} \right)}^{n-1} \right]= {x}^{n}-{y}^{n}\Rightarrow {y}^{n}\left(\frac{x-y}{y} \right)\left[1+\frac{x}{y}+{\left(\frac{x}{y} \right)}^{2}+...+{\left(\frac{x}{y} \right)}^{n-1} \right]= {x}^{n}-{y}^{n}\Rightarrow](/latexrender/pictures/15b4e50dae98cc8b1ce9efe118618abf.png)
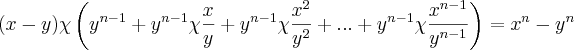
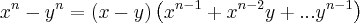
Observação: o símbolo mais apropriado que encontrei para multiplicação foi
, e só utilizei no final da resolução.
Bom, primeiro: aS - S =
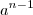

(a-1) S =
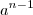

S=
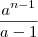
eu realmente não entendi por que aS-S =

. Entendi que o cara multiplicou ambos os membros da igualdade por a, e na subtração a se corta com a, a² se corta com a² mas não entendi por que
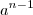
fica fora do resultado da subtração. Ele subtraiu
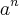
-
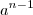
que deu
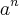
? Não entendi!
Bom,nesta parte da equação
![\left(\frac{x}{y}-1 \right)\left[1+\frac{x}{y}+{\left(\frac{x}{y} \right)}^{2}+...+{\left(\frac{x}{y} \right)}^{n-1} \right]= \frac{{x}^{n}-{y}^{n}}{{y}^{n}} \left(\frac{x}{y}-1 \right)\left[1+\frac{x}{y}+{\left(\frac{x}{y} \right)}^{2}+...+{\left(\frac{x}{y} \right)}^{n-1} \right]= \frac{{x}^{n}-{y}^{n}}{{y}^{n}}](/latexrender/pictures/3aaecbc7bc35c0a88573bc0df4c232bb.png)
esta expressão
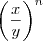
simplesmente some dos colchetes. Por quê?
na penúltima linha, com a equação,
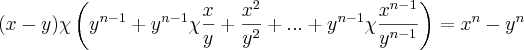
eu já não entendi absolutamente nada. Eu entendi que o cara multiplicou a ambos os membros por
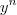
mas não sei como terminou assim.
Bom, é isso. Agradeço muito a quem puder me ajudar a entender. Grato desde já.
-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por MarceloFantini » Qui Jul 19, 2012 00:51
por MarceloFantini » Qui Jul 19, 2012 00:51
Pela definição que ele deu, sabemos que

, ou seja, o último termo é

. Multiplicando tudo por

segue
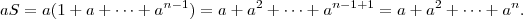
Subtraindo,
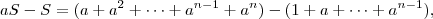
onde os termos de

até

se cancelam, sobrando

.
Perceba então que você deve ter copiado ou lido errado (se não foi um destes casos, o livro está errado mesmo), pois colocando

em evidência e isolando encontramos
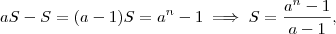
que é a expressão que ele realmente usa. Fazendo
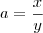
e substituindo,
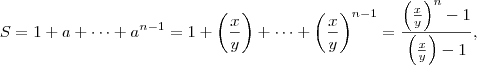
que é a expressão que ele coloca. Vamos simplificar com calma: o numerador
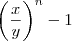
torna-se
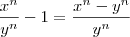
, enquanto que o denominador vira
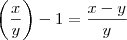
. Multiplicando os dois lados pelo denominador, chegamos na próxima passagem:
![\left( \frac{x-y}{y} \right) \left[ 1 + \left( \frac{x}{y} \right) + \cdots + \left( \frac{x}{y} \right)^{n-1} \right] = \left( \frac{x^n -y^n}{y^n} \right). \left( \frac{x-y}{y} \right) \left[ 1 + \left( \frac{x}{y} \right) + \cdots + \left( \frac{x}{y} \right)^{n-1} \right] = \left( \frac{x^n -y^n}{y^n} \right).](/latexrender/pictures/5de74858546adabaaac2da6fdfd9c19a.png)
Daqui, multiplicamos por
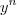
, só que já temos um elemento

dividindo, logo subtraimos os expoentes:
![y^n \cdot \left( \frac{x-y}{y} \right) \left[ 1 + \left( \frac{x}{y} \right) + \cdots + \left( \frac{x}{y} \right)^{n-1} \right] y^n \cdot \left( \frac{x-y}{y} \right) \left[ 1 + \left( \frac{x}{y} \right) + \cdots + \left( \frac{x}{y} \right)^{n-1} \right]](/latexrender/pictures/74d6660c3b683ba23dd1f4848f964ff5.png)
![= \left( \frac{y^n}{y} \right) \cdot (x-y) \left[ 1 + \left( \frac{x}{y} \right) + \cdots + \left( \frac{x}{y} \right)^{n-1} \right] = \left( \frac{y^n}{y} \right) \cdot (x-y) \left[ 1 + \left( \frac{x}{y} \right) + \cdots + \left( \frac{x}{y} \right)^{n-1} \right]](/latexrender/pictures/79b92802e55124b3ff97c9afe9a576fa.png)
![= (x-y) \cdot y^{n-1} \cdot \left[ 1 + \left( \frac{x}{y} \right) + \cdots + \left( \frac{x}{y} \right)^{n-1} \right] = (x-y) \cdot y^{n-1} \cdot \left[ 1 + \left( \frac{x}{y} \right) + \cdots + \left( \frac{x}{y} \right)^{n-1} \right]](/latexrender/pictures/2032bccab2c290b0a5aa0b4a2fbaaf1b.png)
![= (x-y) \cdot \left[ y^{n-1} + \left( x y^{n-2} \right) + \cdots + \left( x^{n-2} y \right) + x^{n-1} \right] = x^n -y^n, = (x-y) \cdot \left[ y^{n-1} + \left( x y^{n-2} \right) + \cdots + \left( x^{n-2} y \right) + x^{n-1} \right] = x^n -y^n,](/latexrender/pictures/e640ec301824444445ba24ddefc0a7a5.png)
e finalmente o que queríamos.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Polinômios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dúvida em exercício de PAG!
 por Fernanda » Qui Jul 03, 2008 18:20
por Fernanda » Qui Jul 03, 2008 18:20
- 11 Respostas
- 10126 Exibições
- Última mensagem por admin

Sex Jul 04, 2008 05:01
Sequências
-
- Dúvida de Exercício
por m0x0 » Qui Jul 21, 2011 16:02
- 8 Respostas
- 4605 Exibições
- Última mensagem por m0x0

Sáb Jul 23, 2011 14:23
Álgebra Elementar
-
- Duvida em Exercício (PUC-SP)
por jrdelazary » Dom Ago 08, 2010 20:30
- 1 Respostas
- 3738 Exibições
- Última mensagem por MarceloFantini

Seg Ago 09, 2010 02:45
Progressões
-
- Exercicio duvida !!!
 por LuizCarlos » Qui Ago 11, 2011 22:43
por LuizCarlos » Qui Ago 11, 2011 22:43
- 3 Respostas
- 2828 Exibições
- Última mensagem por LuizCarlos

Sex Ago 12, 2011 18:57
Álgebra Elementar
-
- Duvida em exercício !
por LuizCarlos » Sex Ago 12, 2011 21:01
- 1 Respostas
- 1615 Exibições
- Última mensagem por Neperiano

Dom Ago 14, 2011 13:21
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 09:10
Veja este exercício:
Se A = {

} e B = {

}, então o número de elementos A

B é:
Eu tentei resolver este exercício e achei a resposta "três", mas surgiram muitas dúvidas aqui durante a resolução.
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero?
existe inverso de zero?
zero é par, certo?
sendo x um número natural, -x é múltiplo de x?
sendo z um número inteiro negativo, z é múltiplo de z?
sendo z um número inteiro negativo, -z é múltiplo de z?
A resposta é 3?
Obrigado.
Assunto:
método de contagem
Autor:
Molina - Seg Mai 25, 2009 20:42
Boa noite, sinuca.
Se A = {

} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
Ou seja, quais são os divisores de 20? Eles são seis: 1, 2, 4, 5, 10 e 20.
Logo, o conjunto A é
A = {1, 2, 4, 5, 10, 20}
Se B = {

} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
Logo, o conjunto B é
B = {... , -25, -20, -15, -10, -5, 0, 5, 10, 15, 20, 25, ...
Feito isso precisamos ver os números que está em ambos os conjuntos, que são:
5, 10 e 20 (3 valores, como você achou).
Vou responder rapidamente suas dúvidas porque meu tempo está estourando. Qualquer dúvida, coloque aqui, ok?
sinuca147 escreveu:No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero? sim, é o próprio zero
existe inverso de zero? não, pois não há nenhum número que multiplicado por zero resulte em 1
zero é par, certo? sim, pois pode ser escrito da forma de 2n, onde n pertence aos inteiros
sendo x um número natural, -x é múltiplo de x? Sim, pois basta pegar x e multiplicar por -1 que encontramos -x
sendo z um número inteiro negativo, z é múltiplo de z? Sim, tais perguntando se todo número é multiplo de si mesmo
sendo z um número inteiro negativo, -z é múltiplo de z? Sim, pois basta pegar -z e multiplicar por -1 que encontramos x
A resposta é 3? Sim, pelo menos foi o que vimos a cima
Bom estudo,

Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 23:35
Obrigado, mas olha só este link
http://www.colegioweb.com.br/matematica ... ro-natural
neste link encontra-se a a frase:
Múltiplo de um número natural é qualquer número que possa ser obtido multiplicando o número natural por 0, 1, 2, 3, 4, 5, etc.
Para determinarmos os múltiplos de 15, por exemplo, devemos multiplicá-lo pela sucessão dos números naturais:
Ou seja, de acordo com este link -5 não poderia ser múltiplo de 5, assim como 5 não poderia ser múltiplo de -5, eu sempre achei que não interessava o sinal na questão dos múltiplos, assim como você me confirmou, mas e essa informação contrária deste site, tem alguma credibilidade?
Há e claro, a coisa mais bacana você esqueceu, quero saber se existe algum método de contagem diferente do manual neste caso:
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
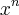 -
- 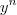 para n inteiro positivo. Bom, eu ''peguei'a prova'' em um livro, mas eu não compreendi alguns artifícios algébricos utilizados pelo autor do livro, por isto estou aqui, para que alguem me ajude a entender. Primeiro vou colocar toda a resolução e depois vou dizer o que não entendi.
para n inteiro positivo. Bom, eu ''peguei'a prova'' em um livro, mas eu não compreendi alguns artifícios algébricos utilizados pelo autor do livro, por isto estou aqui, para que alguem me ajude a entender. Primeiro vou colocar toda a resolução e depois vou dizer o que não entendi.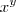 -
- 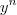 = (x - y) (
= (x - y) ( 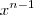 +
+ 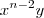 +....+
+....+ 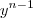 .
. 1,
1, 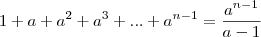
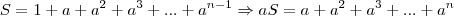

 (a-1) S =
(a-1) S = 
 S=
S= 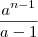
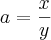 na expressão
na expressão 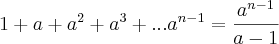 ,
,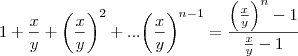

![\left(\frac{x}{y}-1 \right)\left[1+\frac{x}{y}+{\left(\frac{x}{y} \right)}^{2}+...+{\left(\frac{x}{y} \right)}^{n-1}={\left(\frac{x}{y} \right)}^{n} \right]={\left(\frac{x}{y}
\right)}^{n}-1\Rightarrow \left(\frac{x}{y}-1 \right)\left[1+\frac{x}{y}+{\left(\frac{x}{y} \right)}^{2}+...+{\left(\frac{x}{y} \right)}^{n-1}={\left(\frac{x}{y} \right)}^{n} \right]={\left(\frac{x}{y}
\right)}^{n}-1\Rightarrow](/latexrender/pictures/b55b363a766543b698e7d099cd436722.png)
![\left(\frac{x}{y}-1 \right)\left[1+\frac{x}{y}+{\left(\frac{x}{y} \right)}^{2}+...+{\left(\frac{x}{y} \right)}^{n-1} \right]= \frac{{x}^{n}-{y}^{n}}{{y}^{n}} \left(\frac{x}{y}-1 \right)\left[1+\frac{x}{y}+{\left(\frac{x}{y} \right)}^{2}+...+{\left(\frac{x}{y} \right)}^{n-1} \right]= \frac{{x}^{n}-{y}^{n}}{{y}^{n}}](/latexrender/pictures/3aaecbc7bc35c0a88573bc0df4c232bb.png)
![{y}^{n}\left(\frac{x-y}{y} \right)\left[1+\frac{x}{y}+{\left(\frac{x}{y} \right)}^{2}+...+{\left(\frac{x}{y} \right)}^{n-1} \right]= {x}^{n}-{y}^{n}\Rightarrow {y}^{n}\left(\frac{x-y}{y} \right)\left[1+\frac{x}{y}+{\left(\frac{x}{y} \right)}^{2}+...+{\left(\frac{x}{y} \right)}^{n-1} \right]= {x}^{n}-{y}^{n}\Rightarrow](/latexrender/pictures/15b4e50dae98cc8b1ce9efe118618abf.png)
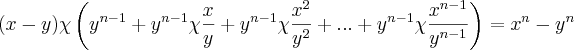
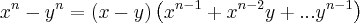
 , e só utilizei no final da resolução.
, e só utilizei no final da resolução.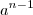
 (a-1) S =
(a-1) S = 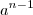
 S=
S= 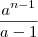
 . Entendi que o cara multiplicou ambos os membros da igualdade por a, e na subtração a se corta com a, a² se corta com a² mas não entendi por que
. Entendi que o cara multiplicou ambos os membros da igualdade por a, e na subtração a se corta com a, a² se corta com a² mas não entendi por que 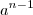 fica fora do resultado da subtração. Ele subtraiu
fica fora do resultado da subtração. Ele subtraiu 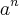 -
- 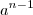 que deu
que deu 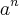 ? Não entendi!
? Não entendi! ![\left(\frac{x}{y}-1 \right)\left[1+\frac{x}{y}+{\left(\frac{x}{y} \right)}^{2}+...+{\left(\frac{x}{y} \right)}^{n-1} \right]= \frac{{x}^{n}-{y}^{n}}{{y}^{n}} \left(\frac{x}{y}-1 \right)\left[1+\frac{x}{y}+{\left(\frac{x}{y} \right)}^{2}+...+{\left(\frac{x}{y} \right)}^{n-1} \right]= \frac{{x}^{n}-{y}^{n}}{{y}^{n}}](/latexrender/pictures/3aaecbc7bc35c0a88573bc0df4c232bb.png) esta expressão
esta expressão 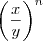 simplesmente some dos colchetes. Por quê?
simplesmente some dos colchetes. Por quê?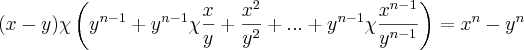 eu já não entendi absolutamente nada. Eu entendi que o cara multiplicou a ambos os membros por
eu já não entendi absolutamente nada. Eu entendi que o cara multiplicou a ambos os membros por 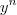 mas não sei como terminou assim.
mas não sei como terminou assim. 

 , ou seja, o último termo é
, ou seja, o último termo é  . Multiplicando tudo por
. Multiplicando tudo por  segue
segue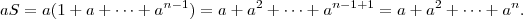
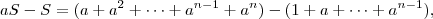
 .
. em evidência e isolando encontramos
em evidência e isolando encontramos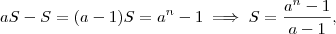
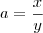 e substituindo,
e substituindo,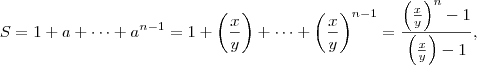
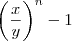 torna-se
torna-se 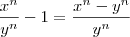 , enquanto que o denominador vira
, enquanto que o denominador vira 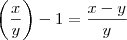 . Multiplicando os dois lados pelo denominador, chegamos na próxima passagem:
. Multiplicando os dois lados pelo denominador, chegamos na próxima passagem:![\left( \frac{x-y}{y} \right) \left[ 1 + \left( \frac{x}{y} \right) + \cdots + \left( \frac{x}{y} \right)^{n-1} \right] = \left( \frac{x^n -y^n}{y^n} \right). \left( \frac{x-y}{y} \right) \left[ 1 + \left( \frac{x}{y} \right) + \cdots + \left( \frac{x}{y} \right)^{n-1} \right] = \left( \frac{x^n -y^n}{y^n} \right).](/latexrender/pictures/5de74858546adabaaac2da6fdfd9c19a.png)
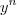 , só que já temos um elemento
, só que já temos um elemento  dividindo, logo subtraimos os expoentes:
dividindo, logo subtraimos os expoentes:![y^n \cdot \left( \frac{x-y}{y} \right) \left[ 1 + \left( \frac{x}{y} \right) + \cdots + \left( \frac{x}{y} \right)^{n-1} \right] y^n \cdot \left( \frac{x-y}{y} \right) \left[ 1 + \left( \frac{x}{y} \right) + \cdots + \left( \frac{x}{y} \right)^{n-1} \right]](/latexrender/pictures/74d6660c3b683ba23dd1f4848f964ff5.png)
![= \left( \frac{y^n}{y} \right) \cdot (x-y) \left[ 1 + \left( \frac{x}{y} \right) + \cdots + \left( \frac{x}{y} \right)^{n-1} \right] = \left( \frac{y^n}{y} \right) \cdot (x-y) \left[ 1 + \left( \frac{x}{y} \right) + \cdots + \left( \frac{x}{y} \right)^{n-1} \right]](/latexrender/pictures/79b92802e55124b3ff97c9afe9a576fa.png)
![= (x-y) \cdot y^{n-1} \cdot \left[ 1 + \left( \frac{x}{y} \right) + \cdots + \left( \frac{x}{y} \right)^{n-1} \right] = (x-y) \cdot y^{n-1} \cdot \left[ 1 + \left( \frac{x}{y} \right) + \cdots + \left( \frac{x}{y} \right)^{n-1} \right]](/latexrender/pictures/2032bccab2c290b0a5aa0b4a2fbaaf1b.png)
![= (x-y) \cdot \left[ y^{n-1} + \left( x y^{n-2} \right) + \cdots + \left( x^{n-2} y \right) + x^{n-1} \right] = x^n -y^n, = (x-y) \cdot \left[ y^{n-1} + \left( x y^{n-2} \right) + \cdots + \left( x^{n-2} y \right) + x^{n-1} \right] = x^n -y^n,](/latexrender/pictures/e640ec301824444445ba24ddefc0a7a5.png)




 } e B = {
} e B = { }, então o número de elementos A
}, então o número de elementos A  B é:
B é: