 por gabrielnandi » Qui Jun 28, 2012 01:25
por gabrielnandi » Qui Jun 28, 2012 01:25
Caso possivel alguem ajudar na resolucao agradeco, estou com muitas dificuldade
Conforme a figura abaixo, suponha que uma vareta com um dos extremos fixos no polo de um sistema de coordenadas polares gire no sentido anti-horario a uma taxa constante de 1Rad/s. No instante t=0 um besouro sobre a vareta esta a 10mm do polo e se movendo para fora ao longo da vareta com uma velocidade constante de 2m/s. Sabendo que a equacao que descreve o caminho percorrido eh: r=20+10, determine a distancia que o besouro percorre durante os 5 primeiros segundos..
abaixo a imagem
- Anexos
-
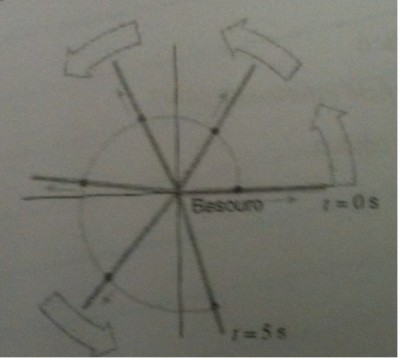
- Imagem mencionada
-
gabrielnandi
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Dom Mai 15, 2011 18:38
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Eletronica
- Andamento: cursando
 por Russman » Qui Jun 28, 2012 08:12
por Russman » Qui Jun 28, 2012 08:12
O ponto de partida é identificar o diferencial de comprimento da trajetória. Este é

.
Portanto, o comprimento total da curva entre os ângulos

e

é dado por

.
Veja que temos duas informações para o problema, quanto ao comportamento da evolução de

e

.

onde

e

são constantes dadas.
Assim,

.
Substituindo na fórmula inicial, temos

.
Portanto, reunindo as informações do problema

.
Logo, para


.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Integrais] Resolução incorreta?
por MrJuniorFerr » Dom Nov 11, 2012 23:04
- 4 Respostas
- 2595 Exibições
- Última mensagem por MrJuniorFerr

Seg Nov 12, 2012 20:34
Cálculo: Limites, Derivadas e Integrais
-
- [Integrais] Exercício - resolução falha
por MrJuniorFerr » Seg Out 29, 2012 00:23
- 5 Respostas
- 2983 Exibições
- Última mensagem por MrJuniorFerr

Seg Out 29, 2012 07:37
Cálculo: Limites, Derivadas e Integrais
-
- [Integrais] Problema com aceleração
por MrJuniorFerr » Sáb Nov 10, 2012 20:19
- 4 Respostas
- 3294 Exibições
- Última mensagem por young_jedi

Sáb Nov 10, 2012 21:37
Cálculo: Limites, Derivadas e Integrais
-
- P.A. resolução de problema
por aliceit » Ter Abr 26, 2011 22:52
- 5 Respostas
- 9831 Exibições
- Última mensagem por MarceloFantini

Qua Abr 27, 2011 23:30
Progressões
-
- ajuda com resolução do problema
por Mimizinha » Qua Mar 19, 2008 16:46
- 2 Respostas
- 2548 Exibições
- Última mensagem por Mimizinha

Qua Mar 19, 2008 17:34
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 .
. e
e  é dado por
é dado por .
. e
e  .
.
 e
e  são constantes dadas.
são constantes dadas. .
. .
. .
.
 .
.

 .
.
 :
: