Calcule a área das curvas y =
 e y =
e y = 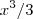 . Note que as duas curvas admitem o mesmo ponto de abcissa 1.
. Note que as duas curvas admitem o mesmo ponto de abcissa 1.Ora o que eu costumava fazer era
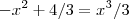 e igualava a zero e depois fazio o integral dos pontos, mas este exercicio é diferente, não sei como aplicar.
e igualava a zero e depois fazio o integral dos pontos, mas este exercicio é diferente, não sei como aplicar.
 e y =
e y = 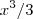 . Note que as duas curvas admitem o mesmo ponto de abcissa 1.
. Note que as duas curvas admitem o mesmo ponto de abcissa 1.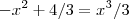 e igualava a zero e depois fazio o integral dos pontos, mas este exercicio é diferente, não sei como aplicar.
e igualava a zero e depois fazio o integral dos pontos, mas este exercicio é diferente, não sei como aplicar.


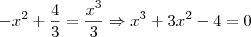 .
. é uma raíz. As outras serão , portanto, calculadas de
é uma raíz. As outras serão , portanto, calculadas de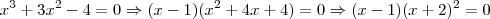 .
. e
e  .
.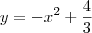 é sempre maior que
é sempre maior que 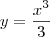 .
.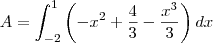 .
.

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes

 .
.
 :
: