por Claudin » Dom Mai 20, 2012 21:45
Determine a equação paramétrica da elipse
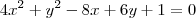
Fiz o seguinte
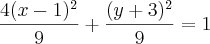
Sabendo que as paramétricas são dadas a partir de:
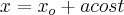
Não sei como prosseguir
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário
-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
por DanielFerreira » Ter Mai 22, 2012 23:30
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação
-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
por Claudin » Qua Mai 23, 2012 21:08
Eu tinha ate conseguido
vi que cometi um erro bobo..
mas mesmo assim valeu ai
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário
-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
por DanielFerreira » Qui Mai 24, 2012 11:02
Vlw.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação
-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
por Claudin » Ter Jun 12, 2012 20:33
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário
-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Elipse
por carmem » Seg Jun 01, 2009 16:21
- 3 Respostas
- 3585 Exibições
- Última mensagem por Cleyson007
Sex Jun 05, 2009 12:54
Geometria Analítica
-
- Elipse
por lucas1365 » Sex Jul 03, 2009 21:30
- 0 Respostas
- 1751 Exibições
- Última mensagem por lucas1365
Sex Jul 03, 2009 21:30
Geometria Analítica
-
- Elipse
por Siax » Sex Jul 10, 2009 00:03
- 0 Respostas
- 1731 Exibições
- Última mensagem por Siax
Sex Jul 10, 2009 00:03
Geometria Analítica
-
- Elipse
por Claudin » Dom Mai 20, 2012 16:46
- 14 Respostas
- 5899 Exibições
- Última mensagem por Claudin
Dom Mai 20, 2012 20:40
Geometria Analítica
-
- Elipse
por Claudin » Dom Mai 20, 2012 18:50
- 2 Respostas
- 1536 Exibições
- Última mensagem por Claudin
Qui Mai 24, 2012 02:55
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25
Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.
Caso ainda não tenha dado uma
, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
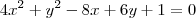
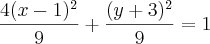
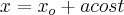
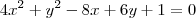
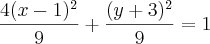
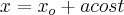
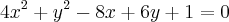
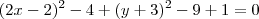
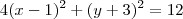
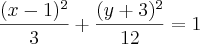
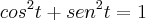,![\frac{(x - 1)^2}{3} = cos^2t ====> \frac{(x - 1)}{\sqrt[]{3}} = cost ====> x = 1 + \sqrt{3}.cost](/latexrender/pictures/6d32537ca178d01fde2b521d30ae48e8.png "\frac{(x - 1)^2}{3} = cos^2t ====> \frac{(x - 1)}{\sqrt[]{3}} = cost ====> x = 1 + \sqrt{3}.cost")
![\frac{(y + 3)^2}{12} = sen^2t ====> \frac{(y + 3)}{2\sqrt[]{3}} = sent====> y = - 3 + 2\sqrt{3}.sent](/latexrender/pictures/b27b497582c318cac5866ae526509471.png "\frac{(y + 3)^2}{12} = sen^2t ====> \frac{(y + 3)}{2\sqrt[]{3}} = sent====> y = - 3 + 2\sqrt{3}.sent")