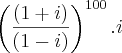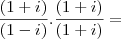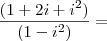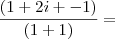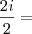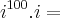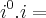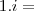por iceman » Dom Mai 27, 2012 21:29
por iceman » Dom Mai 27, 2012 21:29
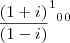
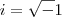
, é igual a:
Tentei escrever pelo Tex mas acho que não deu muito certo.
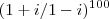
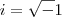
, é igual a:
a) i
b) ?1
c) 1
d) ? i
e) N.D.A
-
iceman
- Usuário Parceiro

-
- Mensagens: 70
- Registrado em: Qui Mai 10, 2012 18:35
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por DanielFerreira » Dom Mai 27, 2012 21:34
por DanielFerreira » Dom Mai 27, 2012 21:34
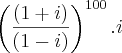
É assim?
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por DanielFerreira » Dom Mai 27, 2012 21:39
por DanielFerreira » Dom Mai 27, 2012 21:39
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por iceman » Dom Mai 27, 2012 22:32
por iceman » Dom Mai 27, 2012 22:32
Não tem os parênteses de dentro, somente os grandes e eu não consigo prosseguir D;
-
iceman
- Usuário Parceiro

-
- Mensagens: 70
- Registrado em: Qui Mai 10, 2012 18:35
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por DanielFerreira » Qui Mai 31, 2012 22:25
por DanielFerreira » Qui Mai 31, 2012 22:25
Então, Iceman,
aquela fração que está dentro do parênteses 'grande' resume-se a
i, com isso:
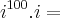
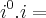
0 => resto da divisão de 100 por 4!!
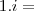

opção "
a"
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Números Complexos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dúvida na minha resolução
por zenildo » Sex Abr 15, 2016 15:10
- 1 Respostas
- 2503 Exibições
- Última mensagem por DanielFerreira

Sáb Abr 23, 2016 15:56
Inequações
-
- [limite trigonometrico]creio que resultado foi coincidencia
por marcosmuscul » Qui Mar 28, 2013 17:23
- 4 Respostas
- 2775 Exibições
- Última mensagem por e8group

Qui Mar 28, 2013 20:19
Cálculo: Limites, Derivadas e Integrais
-
- Última tentativa frustrada de hj - logaritmo
por Fernanda Lauton » Seg Jun 28, 2010 16:16
- 2 Respostas
- 1565 Exibições
- Última mensagem por Fernanda Lauton

Seg Jun 28, 2010 19:30
Logaritmos
-
- Triângulo Qual a última propriedade?
por IsadoraLG » Ter Jul 08, 2014 20:11
- 1 Respostas
- 1685 Exibições
- Última mensagem por e8group

Ter Jul 08, 2014 21:25
Geometria Plana
-
- assunto urgente
por erika kellen vaz » Dom Mar 01, 2015 14:41
- 1 Respostas
- 1829 Exibições
- Última mensagem por Russman

Dom Mar 01, 2015 16:43
Lógica
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
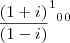
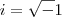 , é igual a:
, é igual a: 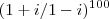
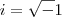 , é igual a:
, é igual a:
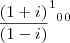
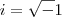 , é igual a:
, é igual a: 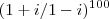
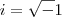 , é igual a:
, é igual a: