arturvr escreveu:Boa noite pessoal, blz? Alguém poderia me ajudar nessa integral:
?(1/R^2) * ((1-r/R)^( 1/7)) rdr
variando de 0 a R.
Você deseja calcular:
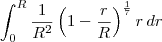
Para estudar uma integral, eu gostaria de lhe dar uma dica. Você pode usar um programa para isso! Por exemplo, o
SAGE, o Mathematica, o Maple, etc.
Alguns desses programas são disponibilizados também na forma de uma página na internet. É o caso do
SAGE Notebook e do Mathematica. Por exemplo, siga os passos abaixo para conferir a resolução da integral indefinida associada a esse problema.
- Acesse a página: http://www.wolframalpha.com/
- No campo de entrada, digite:
- Código: Selecionar todos
integrate (1/R^2)((1-r/R)^( 1/7))r dr
- Clique no botão de igual ao lado do campo de entrada.
- Após a integral ser calculada, clique no botão "Show steps" ao lado do resultado.
- Pronto! Agora basta estudar a resolução.
Depois que você determinou o resultado da integral indefinida, fica fácil calcular a integral definida.
Você também pode conferir o resultado final da integral definida substituindo o código do passo 2 por:
- Código: Selecionar todos
integrate (1/R^2)((1-r/R)^( 1/7))r dr, r=0..R
ObservaçãoEu gostaria de recomendar que você leia o tópico abaixo para saber como digitar de forma adequada todas as notações matemáticas aqui no fórum.
DICA: Escrevendo Fórmulas com LaTeX via BBCodeviewtopic.php?f=9&t=74


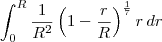


 .
.



