 por LAZAROTTI » Dom Mai 13, 2012 21:45
por LAZAROTTI » Dom Mai 13, 2012 21:45
Boa noite,
Gostaria de conferir algumas questões de Limites.
a)
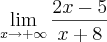
encontrei o resultado
2b)
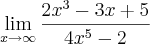
encontrei o resultado
0Está correto?
Abraços,
Allan Lazarotti
-
LAZAROTTI
- Usuário Ativo

-
- Mensagens: 22
- Registrado em: Ter Mai 01, 2012 13:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por LuizAquino » Seg Mai 14, 2012 10:23
por LuizAquino » Seg Mai 14, 2012 10:23
LAZAROTTI escreveu:Boa noite,
Gostaria de conferir algumas questões de Limites.
a)
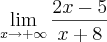
encontrei o resultado
2b)
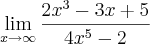
encontrei o resultado
0Está correto?
Para conferir a sua resposta, você pode usar um programa. Por exemplo, o
SAGE, o Mathematica, o Maple, etc.
Alguns desses programas são disponibilizados também na forma de uma página na internet. É o caso do
SAGE Notebook e do Mathematica. Por exemplo, siga os passos abaixo para conferir o resultado desses limites.
- Acesse a página: http://www.wolframalpha.com/
- No campo de entrada, digite:
- Código: Selecionar todos
limit (2x - 5)/(x + 8) as x->+infinity
- Clique no botão de igual ao lado do campo de entrada.
- Espere aparecer o resultado do limite.
- Pronto!
Para conferir o segundo limite, basta usar o código:
- Código: Selecionar todos
limit (2x^3 - 3x + 5)/(4x^5 - 2) as x->+infinity
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Cálculo: Limites, Derivadas e Integrais] Cálculo de limites
por jeferson lopes » Ter Mar 26, 2013 08:49
- 2 Respostas
- 5569 Exibições
- Última mensagem por jeferson lopes

Ter Mar 26, 2013 11:52
Cálculo: Limites, Derivadas e Integrais
-
- [limites] exercicio de calculo envolvendo limites
por lucasdemirand » Qua Jul 10, 2013 00:45
- 1 Respostas
- 4812 Exibições
- Última mensagem por e8group

Sáb Jul 20, 2013 13:08
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo 2 - Limites] Existência de Limites
por Piva » Seg Abr 16, 2012 11:29
- 0 Respostas
- 5448 Exibições
- Última mensagem por Piva

Seg Abr 16, 2012 11:29
Cálculo: Limites, Derivadas e Integrais
-
- cálculo de limites
por Hansegon » Seg Ago 25, 2008 11:29
- 2 Respostas
- 59836 Exibições
- Última mensagem por Guill

Dom Abr 08, 2012 16:03
Cálculo: Limites, Derivadas e Integrais
-
- Calculo de limites
por Emanuel_27 » Sáb Nov 01, 2008 01:57
- 3 Respostas
- 7154 Exibições
- Última mensagem por Molina

Qui Abr 09, 2009 22:47
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
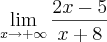 encontrei o resultado 2
encontrei o resultado 2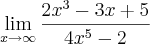 encontrei o resultado 0
encontrei o resultado 0
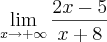 encontrei o resultado 2
encontrei o resultado 2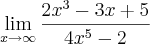 encontrei o resultado 0
encontrei o resultado 0
encontrei o resultado 2
encontrei o resultado 0
