danjr5 escreveu:Sim. É esse o caminho!!
Se não errei nada dá 5, confere aí.
Olá amigo danjr5, encontrei o resultado
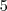
também, está certo com o gabarito! deixa eu ti pergunta, encontrei outra raiz também, sendo

, a segunda raiz encontrada também está correta, isso é uma pergunta, pois meu teclado é complicado para encontrar o ponto de interrogação.
Mas como é medida, então não existe medida negativa, então devo desconsiderar essa raiz, e pegar somente a primeira raiz, que é positiva, correto.
Outra pergunta! geralmente esses problemas, questões, são assim, você deve considerar a raiz que tenha haver com o problema em questão, a raiz que seja conveniente, esse é o pensamento correto. Obrigado amigo danjr5, você é muito legal!

 por
por  e, ao seu redor, uma faixa de madeira de uma certa largura.Se a área dessa mesa é
e, ao seu redor, uma faixa de madeira de uma certa largura.Se a área dessa mesa é  ,qual é a largura da faixa de madeira.
,qual é a largura da faixa de madeira.


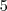 também, está certo com o gabarito! deixa eu ti pergunta, encontrei outra raiz também, sendo
também, está certo com o gabarito! deixa eu ti pergunta, encontrei outra raiz também, sendo  , a segunda raiz encontrada também está correta, isso é uma pergunta, pois meu teclado é complicado para encontrar o ponto de interrogação.
, a segunda raiz encontrada também está correta, isso é uma pergunta, pois meu teclado é complicado para encontrar o ponto de interrogação. 

 .
.
 :
: