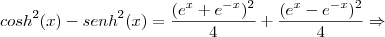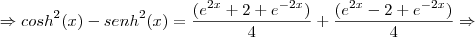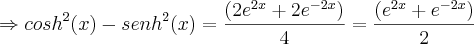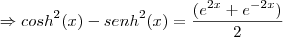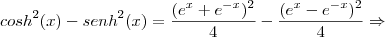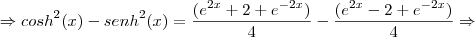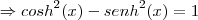por MERLAYNE » Qui Abr 26, 2012 17:00
por MERLAYNE » Qui Abr 26, 2012 17:00
(Ufg 2006) Certas combinações entre as funções
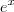
e

. (onde "e" é o número de Euler, x

|R) surgem em diversas áreas, como Matemática, Engenharia e Física. O seno hiperbólico e o cosseno hiperbólico são definidos por:
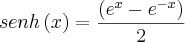
e
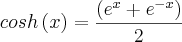
Então,
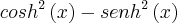
é igual a:
PS: NÃO SEI O QUE É COSSENO E SENO HIPERBOLICO
-
MERLAYNE
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Qua Mar 28, 2012 19:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por nakagumahissao » Qui Abr 26, 2012 20:21
por nakagumahissao » Qui Abr 26, 2012 20:21
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
 por DanielFerreira » Qui Abr 26, 2012 20:27
por DanielFerreira » Qui Abr 26, 2012 20:27
O sinal entre as frações é
negativo!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por nakagumahissao » Qui Abr 26, 2012 20:53
por nakagumahissao » Qui Abr 26, 2012 20:53
Tem toda razão danjr., Obrigado.
Eis a resolução correta:
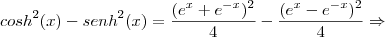
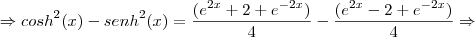
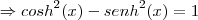
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
 por DanielFerreira » Qui Abr 26, 2012 20:56
por DanielFerreira » Qui Abr 26, 2012 20:56
vlw.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por MERLAYNE » Qua Mai 09, 2012 10:59
por MERLAYNE » Qua Mai 09, 2012 10:59
perfeito! muito obrigada ;D
-
MERLAYNE
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Qua Mar 28, 2012 19:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Relações
por Rose » Qui Mai 15, 2008 14:41
- 1 Respostas
- 1957 Exibições
- Última mensagem por admin

Qui Mai 15, 2008 16:38
Funções
-
- Relações
por chronoss » Seg Mai 20, 2013 14:19
- 0 Respostas
- 1043 Exibições
- Última mensagem por chronoss

Seg Mai 20, 2013 14:19
Álgebra Elementar
-
- Relações
por livia02 » Qua Set 04, 2013 17:15
- 0 Respostas
- 1118 Exibições
- Última mensagem por livia02

Qua Set 04, 2013 17:15
Álgebra Elementar
-
- [Relações]
por Giudav » Ter Fev 11, 2014 18:38
- 1 Respostas
- 2554 Exibições
- Última mensagem por DanielFerreira

Qua Fev 12, 2014 17:47
Sequências
-
- Relações no círculo
por RBenicio » Qua Set 16, 2009 15:34
- 3 Respostas
- 2822 Exibições
- Última mensagem por Molina

Qui Set 17, 2009 14:45
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
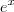 e
e  . (onde "e" é o número de Euler, x
. (onde "e" é o número de Euler, x  |R) surgem em diversas áreas, como Matemática, Engenharia e Física. O seno hiperbólico e o cosseno hiperbólico são definidos por:
|R) surgem em diversas áreas, como Matemática, Engenharia e Física. O seno hiperbólico e o cosseno hiperbólico são definidos por: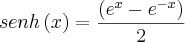 e
e 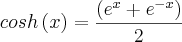
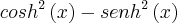 é igual a:
é igual a:
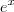 e
e  . (onde "e" é o número de Euler, x
. (onde "e" é o número de Euler, x  |R) surgem em diversas áreas, como Matemática, Engenharia e Física. O seno hiperbólico e o cosseno hiperbólico são definidos por:
|R) surgem em diversas áreas, como Matemática, Engenharia e Física. O seno hiperbólico e o cosseno hiperbólico são definidos por: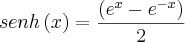 e
e 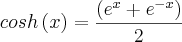
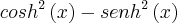 é igual a:
é igual a: