 por LuizCarlos » Ter Mai 08, 2012 11:47
por LuizCarlos » Ter Mai 08, 2012 11:47
Olá amigos professores!
Estou com uma dúvida, em um problema!
Um retângulo tem
![\sqrt[]{12}m \sqrt[]{12}m](/latexrender/pictures/9ae384aa08395f0e173e5decf86a0c15.png)
de largura e
![\sqrt[]{27}m \sqrt[]{27}m](/latexrender/pictures/296e8a4f8e791514b4c087988f24b7f2.png)
de comprimento.Qual é a área desse retângulo.
Consegui resolver, porém estou com uma dúvida!
![\sqrt[]{12}m . \sqrt[]{27}m = \sqrt[]{12m.27m} = \sqrt[]{324{m}^{2}} = 18m \sqrt[]{12}m . \sqrt[]{27}m = \sqrt[]{12m.27m} = \sqrt[]{324{m}^{2}} = 18m](/latexrender/pictures/71656cd628e93dfce43e8be6ae9a390d.png)
A resposta no livro é em
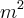
, porém a minha resposta é em

, pois o
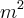
, cancela com o índice da raiz! mas como ele pede a área, e área é em
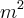
, então devo considerar como
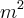
, seria isso.
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por Russman » Ter Mai 08, 2012 14:40
por Russman » Ter Mai 08, 2012 14:40
Nãao! A unidade "metro" NÃO está dentro da raiz! Comprimento se mede em metro, não raiz quadrada do mesmo.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por LuizCarlos » Ter Mai 08, 2012 15:50
por LuizCarlos » Ter Mai 08, 2012 15:50
Russman escreveu:Nãao! A unidade "metro" NÃO está dentro da raiz! Comprimento se mede em metro, não raiz quadrada do mesmo.
Valeu amigo Russman, consegui entender!

-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Problemas equação 1° grau, dúvida.
por Clairelz12 » Sáb Ago 29, 2009 03:44
- 4 Respostas
- 7477 Exibições
- Última mensagem por Elcioschin

Sáb Ago 29, 2009 19:18
Álgebra Elementar
-
- Dúvida em exercício proporções e problemas
por LuizCarlos » Dom Abr 08, 2012 08:00
- 2 Respostas
- 1840 Exibições
- Última mensagem por LuizCarlos

Dom Abr 08, 2012 22:00
Álgebra Elementar
-
- Dúvida 2 Problemas de probabilidade basica
por feperessim » Sáb Ago 27, 2016 19:13
- 0 Respostas
- 2976 Exibições
- Última mensagem por feperessim

Sáb Ago 27, 2016 19:13
Probabilidade
-
- Dúvida em relação aos três problemas clássicos
por Guga1981 » Seg Ago 27, 2018 01:01
- 1 Respostas
- 6844 Exibições
- Última mensagem por Guga1981

Qua Ago 29, 2018 19:17
Geometria Plana
-
- Problemas de MMC
por Gisele Rocha » Qua Jun 24, 2009 12:33
- 2 Respostas
- 4553 Exibições
- Última mensagem por Gisele Rocha

Qua Jun 24, 2009 16:28
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[]{12}m \sqrt[]{12}m](/latexrender/pictures/9ae384aa08395f0e173e5decf86a0c15.png) de largura e
de largura e ![\sqrt[]{27}m \sqrt[]{27}m](/latexrender/pictures/296e8a4f8e791514b4c087988f24b7f2.png) de comprimento.Qual é a área desse retângulo.
de comprimento.Qual é a área desse retângulo.![\sqrt[]{12}m . \sqrt[]{27}m = \sqrt[]{12m.27m} = \sqrt[]{324{m}^{2}} = 18m \sqrt[]{12}m . \sqrt[]{27}m = \sqrt[]{12m.27m} = \sqrt[]{324{m}^{2}} = 18m](/latexrender/pictures/71656cd628e93dfce43e8be6ae9a390d.png)
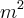 , porém a minha resposta é em
, porém a minha resposta é em  , pois o
, pois o 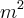 , cancela com o índice da raiz! mas como ele pede a área, e área é em
, cancela com o índice da raiz! mas como ele pede a área, e área é em 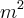 , então devo considerar como
, então devo considerar como 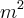 , seria isso.
, seria isso.

