Tenho dificuldades em "visualizar" os intervalos nos quadrantes do círculo trigonométrico
Por exemplo:
]-pi;pi[
]-pi/2;pi/2[ Como faço para ver se é no 1º,2º,3º ou 4º quadrante?
]0;-3pi/2[
]-pi/2;pi[
por anamendes » Dom Mai 06, 2012 09:10
por Molina » Ter Mai 08, 2012 00:28
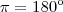. Talvez assim você visualize melhor.
por Jhenrique » Qui Nov 01, 2012 21:39
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
(dica : igualar a expressão a 
e elevar ao quadrado os dois lados)